Genomgång

Övningar

Facit

Nästa avsnitt >>

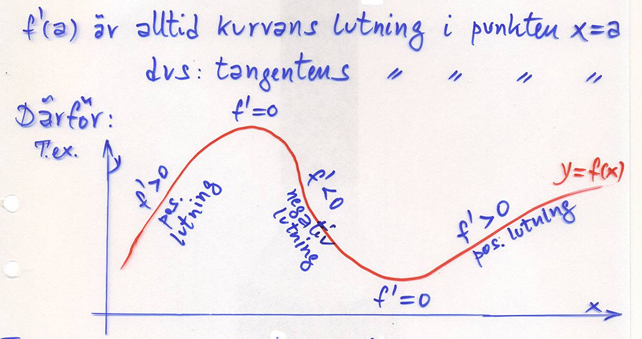
Derivatan = Kurvans lutning = Tangentens lutning

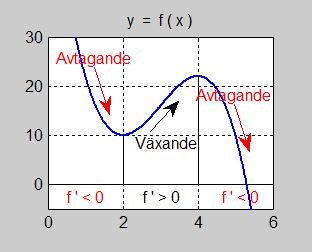
Växande och avtagande

Det handlar om att använda derivatan som ett verktyg för att få information om själva funktionen.

Här används derivatan för att få reda på om funktionen växer eller avtar.

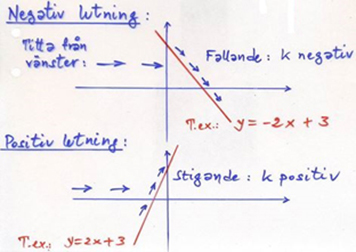
Negativ och positiv lutning hos räta linjer och kurvor:

Regler om en funktions växande och avtagande

Det är derivatans tecken (\( \,+\, \) eller \( \,-\, \)) som avgör om en funktion är växande eller avtagande.

Funktionen \( \; y \, = \, f(x) \; \) är växande för \( \; x = a \; \) om derivatan \( \; f\,'(a) \, {\bf {\color{Red} >}} \, 0 \;. \)

Funktionen \( \; y \, = \, f(x) \; \) är avtagande för \( \; x = a \; \) om derivatan \( \; f\,'(a) \, {\bf {\color{Red} <}} \, 0 \;. \)

Kortfattat:

\( \quad \)

Derivatan positiv i en punkt \( \quad\; \iff \quad \) Funktionen växer där.

Derivatan negativ i en punkt \( \quad \iff \quad \) Funktionen avtar där.

Om derivatan \( \, f\,'(a) \; {\bf {\color{Red} =}} \; 0 \, \) är funktionen varken växande eller avtagande för \( \, x = a \), se Lokala maxima och minima.

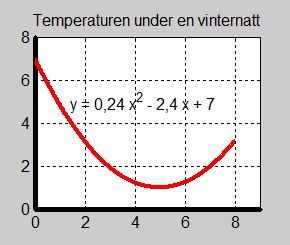
Exempel 1 Vinternatt

Under en vinternatt varierar temperaturen enligt funktionen

\[ y \, = \, f(x) \, = \, 0,24\,x^2\,-\,2,4\,x\,+\,7 \]

där \( y \;\, = \) temperaturen i grader Celsius och

\( x \;\, = \) tiden i timmar efter midnatt

Funktionen \(\, f(x)\):s definitionsmängd: \( \quad 0 \leq x \leq 8 \)

a) Avgör algebraiskt om temperaturen är växande eller avtagande vid:

kl 2 kl 5 kl 7

b) Rita graferna till \( \, f(x) \, \) och \( \, f\,'(x) \). Tolka graferna.

Påminnelse: En funktions definitionsmängd är mängden av alla \( \, x \, \) för vilka funktionen är definierad.

Lösning:

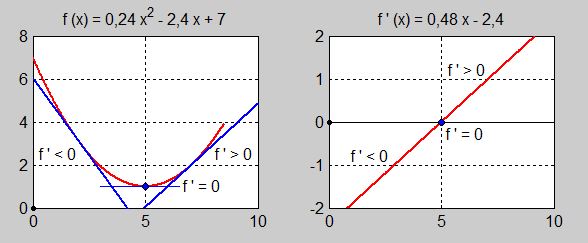
a) För att kunna använda reglerna ovan ställer vi upp derivatan:

\[ f(x) \, = \, 0,24\,x^2 - 2,4\,x + 7 \]

\[ f'(x) \, = \, 0,48\,x - 2,4 \]

För att bestämma derivatans tecken måste vi beräkna derivatans värden för de efterfrågade tiderna:

\( f'(2) \, = \, 0,48 \cdot 2 - 2,4 = -1,44 < 0 \; \Rightarrow \; \) Temperaturen är avtagande vid kl 2.

\( f'(5) \, = \, 0,48 \cdot 5 - 2,4 \qquad\qquad\! = \, 0 \; \Rightarrow \; \) Temperaturen är varken växande eller avtagande vid kl 5.

\( f'(7) \, = \, 0,48 \cdot 7 - 2,4 = \;\;\, 0,96 > 0 \; \Rightarrow \; \) Temperaturen är växande vid kl 7.

b)

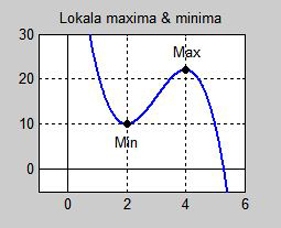
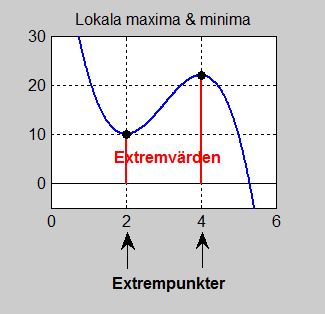
Lokala maxima och minima

Lokala maxima och minima är punkter som har största

resp. minsta funktionsvärden i sin närmaste omgivning.

Med maxima och minima menas i detta kapitel alltid

lokala maxima och minima.

Globala maxima och minima är punkter som har största

resp. minsta y-värden i f(x):s hela definitionsområde.

Se även Begreppsförklaringar.

\( \quad \)

För att avgöra vilka nollställen av derivatan som är funktionens maxima och

vilka som är minima \( \ldots \, \), undersöker man derivatans teckenbyte i nollställena.

Det finns två metoder för att göra denna undersökning:

Teckenstudie som vi börjar med,

Andraderivatan som tas upp längre fram.

Regler om max/min med teckenstudie

\( f\,'(a) \, = \, 0 \; \) och \( \; f\,'(x) \; \) byter tecken från \( \, + \, \) till \( \, - \, \) i \( \, x = a \quad \Longrightarrow \quad f(x) \, \) har ett maximum i \( \, x = a \, \).

\( f\,'(a) \, = \, 0 \; \) och \( \; f\,'(x) \; \) byter tecken från \( \, - \, \) till \( \, + \, \) i \( \, x = a \quad \Longrightarrow \quad f(x) \, \) har ett minimum i \( \, x = a \, \).

\( f\,'(a) \, = \, 0 \; \) och \( \; f\,'(x) \; \) byter inte tecken i \( \, x = a \quad \Longrightarrow \quad f(x) \, \) har en terasspunkt i \( \, x = a \), se Matte 3c, 3.3. Terasspunkter.

En alternativ metod för att skilja mellan funktionens maxima och minima är andraderivatan.

Till skillnad från teckenstudie som klarar sig med första derivatan, måste vi derivera här två gånger.

En fördel med metoden med andraderivatan är dock att den kräver mindre räkning.

Andraderivata

Med andraderivata menas derivatans derivata som betecknas med \( \, f\,''(x) \, \) och läses \( \; {\rm "}\!f \; {\rm biss\;av\; } x\,{\rm"} \, \).

Man får andraderivatan genom att derivera derivatans funktion en gång till enligt deriveringsreglerna.

Det är derivatans nollställen och andraderivatans tecken i derivatans nollställen som avgör om en funktion har maxima eller minima:

Regler om max/min med andraderivatan

\( f\,'(a) \, {\bf {\color{Red} =}} \, 0 \; \) och \( \; f\,''(a) \, {\bf {\color{Red} <}} \, 0 \quad \Longrightarrow \quad \) Funktionen \( \; y = f(x) \; \) har ett maximum i \( \; x = a \; \).

\( f\,'(a) \, {\bf {\color{Red} =}} \, 0 \; \) och \( \; f\,''(a) \, {\bf {\color{Red} >}} \, 0 \quad \Longrightarrow \quad \) Funktionen \( \; y = f(x) \; \) har ett minimum i \( \; x = a \; \).

Om \( \, f\,'(a) = f\,''(a) = 0 \, \) kan endast en korrekt teckenstudie eller \( \, f\,'''(a) \, \) avgöra saken.

Begreppsförklaringar

Lokala maxima och minima är punkter (•) på kurvan som har största resp. minsta \( \, y\)-

värden i sin närmaste omgivning.

Med maxima och minima menas i detta kapitel alltid lokala maxima/minima.

Båda tillsammans heter extrema. Man skiljer mellan extremas \( \, x\)- och \( \, y\)-koordinater:

Extremas \( \, x\,\)-koordinater kallas för extrempunkter, på bilden: \( \; 2 \; \) och \( \;\; 4 \).

Extremas \( \, {\color{Red} y}\,\)-koordinater kallas för extremvärden, på bilden: \( \, 10 \, \) och \( \, 22 \).

Här pratar vi om funktionens extrempunkter och extremvärden. På funktionens graf är:

minimipunktens koordinater: \( \, (2, 10) \, \) och maximipunktens koordinater: \( \, (4, 22) \, \).

Att vara maximi- eller minimipunkt kallas för extrempunktens karaktär eller typ.

I hela detta kapitel förutsätts att varje funktion \( \, y = f(x) \, \) är kontinuerlig i alla punkter av sin definitionsmängd.

Påminnelse: En funktions definitionsmängd är mängden av alla \( \, x \, \) för vilka funktionen är definierad.

OBS! Det finns punkter där derivatan är \( \, 0 \), utan att dessa punkter är extrempunkter. De behandlas i Matte 3c, 3.3. Terasspunkter.

2.7 Grafer och derivator