4.1 Olika typer av tal
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
Genomför: Enkät kursutvärdering
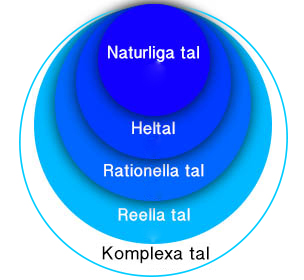
Repetition: Olika typer av tal
|
Vi brukar räkna antalet saker och ting i vår omgivning med den enklaste typen av tal, de positiva heltalen:\(\qquad\qquad\qquad\qquad\) Så räknar vi antal objekt i en mängd, t.ex. fingrarna i våra händer. Alla dessa tal är \( \, > 0 \), medan själva \( \, 0 \, \) får man först genom att dra av två lika stora positiva tal från varandra, t.ex. \( \, 4 - 4 = 0 \, \). Detta leder till en ny talmängd med de positiva heltalen och \( 0 \), kallad: Naturliga tal:
 Drar man av ett större naturligt tal från ett mindre kommer man till negativa tal, t.ex. \( \, 4 - 5 = -1 \). Så uppstår ytterligare en ny talmängd: Heltal:
 Division av två heltal med varandra, t.ex. \( \, 1 / 3 = \displaystyle{1 \over 3} \, \) leder till tal i bråkform, även kallade: |
Lökmodell: De olika taltyperna är delmängder av varandra.
|
Rationella tal är tal i bråkform och kan alltid skrivas i decimalform. Dock finns decimaltal som inte kan skrivas i bråkform.
Exempel Drar man roten ur \( \, 2 \, \) kommer man till: \( \qquad \sqrt{2} = 1,4142135623730950488\ldots \quad\) (Diagonalen i en kvadrat med sidlängden 1).
\( \sqrt{2} \, \) kan inte anges i bråkform \(-\) är inget rationellt tal \(-\) därför att det har oändligt många decimaler utan något upprepande mönster (utan period).
Sådana tal kallas för irrationella tal och är decimaltal med en oändlig icke-periodisk decimalutveckling. \( \sqrt{2} \, \), \( \sqrt{3} \, \) och talet \( \, \pi \, \) är exempel på irrationella tal.
Matematiskt exakt talat, är \( \, \sqrt{2} \, \) gränsvärdet (limes) av en följd av rationella tal som i varje steg närmar sig \( \, \sqrt{2} \).
Gränsvärdet själv: \( \, \sqrt{2} \, \) är inte längre rationellt utan ligger utanför den rationella talmängden.
Därför inför man en ny typ av tal och kallar dem för:
Den här gången leder operationen gränsvärdesbildning till en ny typ av tal: mängden av alla reella tal.
Men det finns ytterligare en talmängd som är ännu mer omfattande än de reella talen.
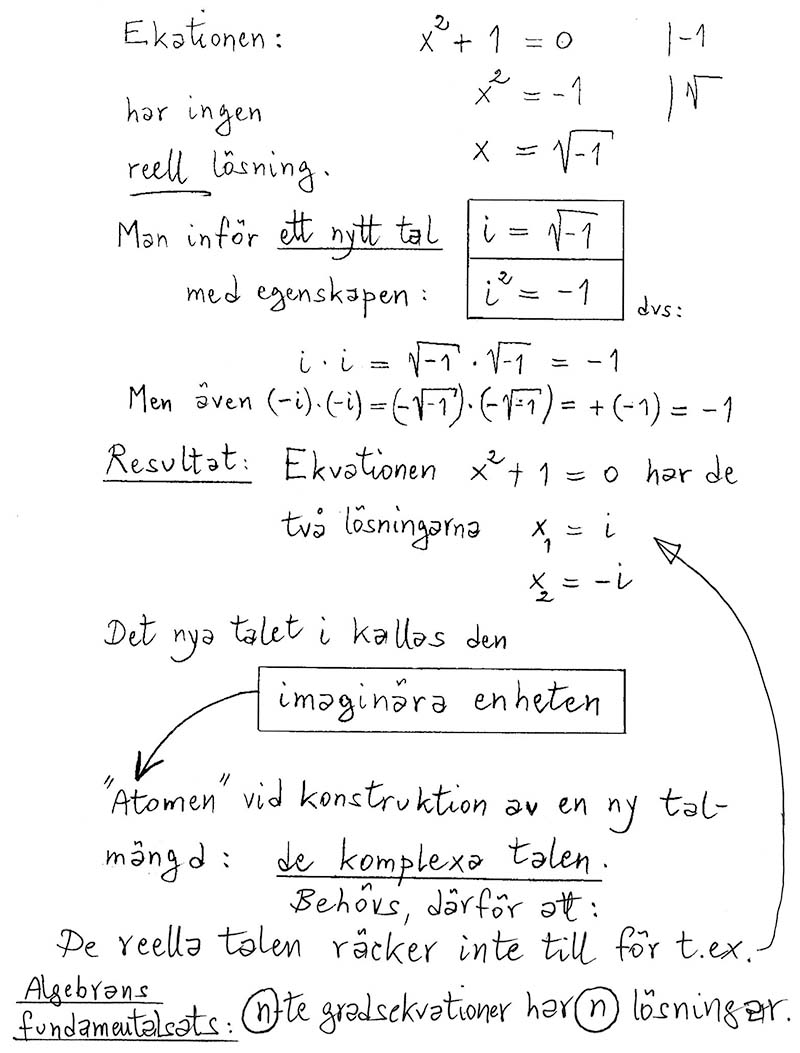
Löser man t.ex. ekvationenVi säger: ekvationen saknar reell lösning.
För att lösa detta dilemma inför vi en ny symbol \( \; {\color{Red} i} \, = \, \sqrt{-1} \; \) med egenskapen \( \; {\color{Red} i}\,^2 \, = \, -1 \; \) och definierar den nya talmängden med hjälp av den nya symbolen:
Symbolen \( \, {\color{Red} i} \, \) är ett exempel på abstraktion, en tankeprocess som alla talmängder i lökmodellen ovan bygger sin konstruktion på och är resultatet av.
Läs mer om detta i avsnittet Om tal.
Komplexa tal
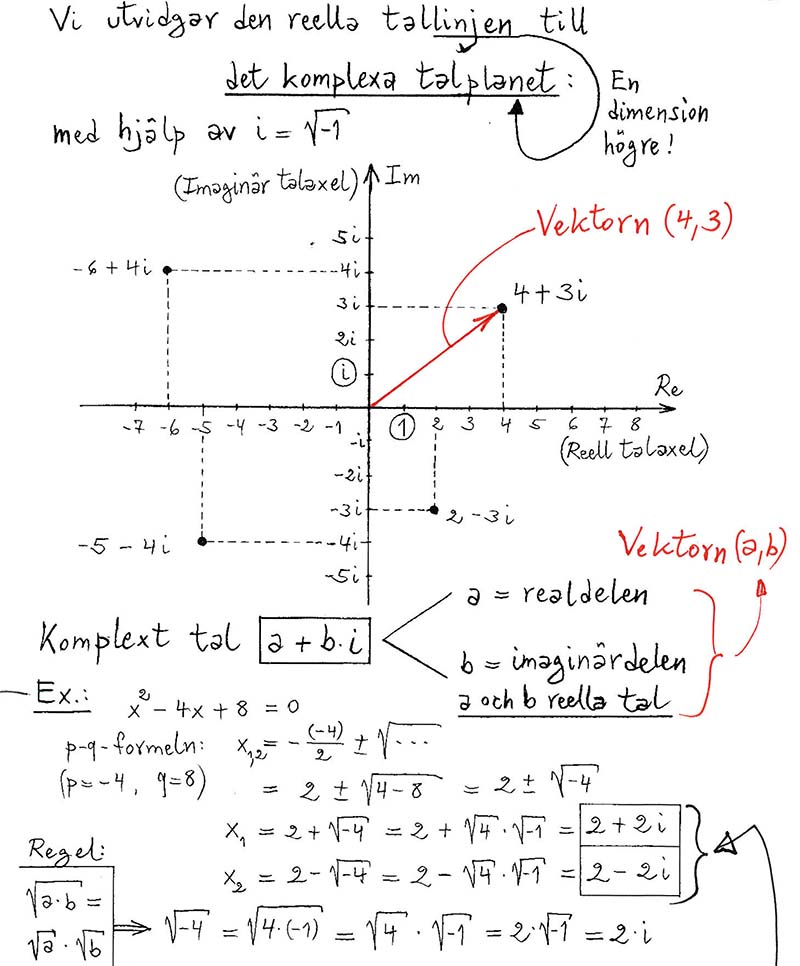
Det komplexa talplanet
| << Förra avsnitt | Genomgång | Övningar | Nästa avsnitt >> |
4.2 Algebrans fundamentalsats
Ett polynom av grad \( n\, \) har exakt \( n\, \) komplexa nollställen \( \; x_1, \, x_2, \,\ldots\, , x_n \), även kallade polynomets rötter.
Polynomet kan fullständigt faktoriseras till exakt \( n\, \) linearfakrorer:
\( a_n x^n + a_{n-1} x^{n-1} + \; \ldots \; + a_1 x + a_0 \; = \; {\color{Red} {a_n \cdot\, (x-x_1) \cdot (x-x_2) \cdot\;\ldots\; \cdot (x-x_n)}} \)
om man räknar rötterna med multiplicitet (dubbla rötter dubbelt osv.), och tar även med de komplexa rötterna.
Utan komplexa tal hade denna faktorisering inte varit möjlig.
Läs mer om Algebrans fundamentalsats samt bevis, historia & annat gott.
Repetera även Faktorisering av polynom från Matte 3c-kursen.
Exempel 1
Faktorisera följande polynom fullständigt:\( \qquad\qquad P(x) = x^4 - 29\;x^2 + 100 \)
I övning 6 hade vi löst 4:e gradsekvationen \( \qquad\qquad\quad\;\; x^4 - 29\,x^2 + 100 \, = \, 0 \)
och fått lösningarna \( \qquad\qquad\qquad\qquad x_1 = 5, \qquad x_2 = -5, \qquad x_3 = 2 \quad {\rm och} \quad x_4 = -2 \)
Pga kännedomen om ekvationens lösningar som är identiska med polynomets nollställen (= rötter), kan vi enligt algebrans fundamentalsats faktorisera 4:e gradspolynomet \( P(x)\, \) så här:
\( \qquad\qquad\qquad\qquad P(x) = x^4 - 29\;x^2 + 100 = (x-5) \cdot (x+5) \cdot (x-2) \cdot (x+2) \)
Exempel 2
Faktorisera polynomet \( P(x)\, \) fullständigt när följande delfaktorisering redan existerar:
- \[ P(x) = x^5 - 5\,x^4 + 17\,x^3 - 13\,x^2 = x\cdot x\cdot (x-1)\cdot (x^2 - 4\,x + 13) \]
Delfaktoriseringen visar en dubbelrot \( x = 0\, \) och en enkel rot \( x = 1\, \). Man kan få fram den med de metoder vi lärt oss i detta avsnitt: Den dubbla roten \( x = 0\, \) får man genom att bryta ut \( x^2 \). Den enkla roten \( x = 1\, \) kan man få via grafen samt en prövning. Den sista faktorn kan beräknas med hjälp av jämförelse av koefficienter. Denna delfaktorisering stannar inom ramen av de reella talen.
Enligt algebrans fundamentalsats måste 5:e gradspolynomet \( P(x)\, \) ha två rötter till som ger upphov till den kvadratiska faktorn \( x^2 - 4\,x + 13 \) som står sist.
Vill man gå vidare och få fram den fullständiga faktoriseringen i linjära faktorer måste även den kvadratiska faktorn faktoriseras. Detta innebär att vi måste beräkna dess rötter som visar sig vara komplexa:
- \[\begin{array}{rcl} x^2 - 4\,x + 13 & = & 0 \\ x_{1,2} & = & 2 \pm \sqrt{4 - 13} \\ x_{1,2} & = & 2 \pm \sqrt{-9} \\ x_{1,2} & = & 2 \pm \sqrt{9 \cdot (-1)} \\ x_{1,2} & = & 2 \pm \sqrt{9}\cdot \sqrt{-1} \\ x_1 & = & 2 + 3\,i \\ x_2 & = & 2 - 3\,i \\ \end{array}\]
Vi får alltså följande faktorisering av den kvadratiska faktorn:
- \[ x^2 - 4\,x + 13 = (x - (2+3\,i)) \cdot (x - (2-3\,i)) = (x - 2-3\,i) \cdot (x - 2+3\,i)\]
Därmed blir den fullständiga faktoriseringen av polynomet \( P(x)\, \) i linjära faktorer\[ P(x) = x^5 - 5\,x^4 + 17\,x^3 - 13\,x^2 = x\cdot x\cdot (x-1)\cdot (x - 2-3\,i) \cdot (x - 2+3\,i) \]
Dvs \( P(x)\, \) har förutom dubbelroten \( x = 0\, \) och den enkla roten \( x = 1\, \) även de två komplexa rötterna \( x = 2 + 3\,i \) och \( x = 2 - 3\,i \). Sammanlagt har 5:e gradspolynomet \( P(x)\, \) exakt 5 rötter, om man räknar rötterna med multiplicitet, dvs den dubbla rötter dubbelt och beräknar även de komplexa rötterna - i enlighet med algebrans fundamentalsats.
Övningar 4111-4113 & Historik 1-3.
Copyright © 2022 TechPages AB. All Rights Reserved.
