2.7 Grafer och derivator
IND_VAL: v46 II, tor kl 14.40-15.50, sal 2
| << Förra avsnitt 3.1 | Genomgång | Övningar | Facit | Nästa avsnitt 3.5 Differentialekvationer >> |
Derivatan = Kurvans lutning = Tangentens lutning
Växande och avtagande
Kapitel 3 handlar om att använda derivatan som ett verktyg för att få information om själva funktionen.
I detta första avsnitt används derivatan för att få reda på om funktionen växer eller avtar.
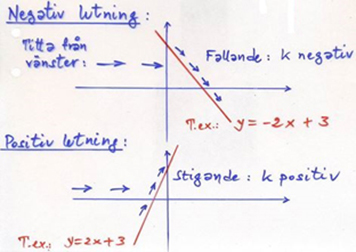
Negativ och positiv lutning hos räta linjer och kurvor:
 |
 |
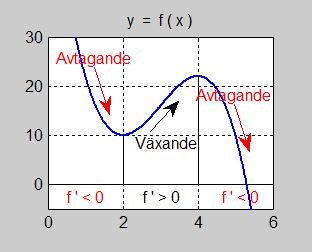Regler om en funktions växande och avtagande
Det är derivatans tecken (\( \,+\, \) eller \( \,-\, \)) som avgör om en funktion är växande eller avtagande.
| Funktionen \( \; y \, = \, f(x) \; \) är växande för \( \; x = a \; \) om derivatan \( \; f\,'(a) \, {\bf {\color{Red} >}} \, 0 \;. \)
Funktionen \( \; y \, = \, f(x) \; \) är avtagande för \( \; x = a \; \) om derivatan \( \; f\,'(a) \, {\bf {\color{Red} <}} \, 0 \;. \)
|
Om derivatan \( \, f\,'(a) \; {\bf {\color{Red} =}} \; 0 \, \) är funktionen varken växande eller avtagande för \( \, x = a \, \). Vilka slutsatser man kan dra då, behandlas i nästa avsnitt.
I exemplen 1-3 visas hur man beräknar för vilka \( \, x \, \) en funktion är växande resp. avtagande.
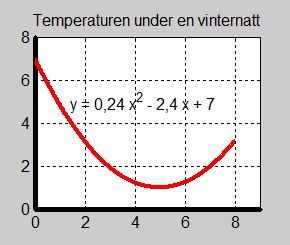
Exempel 1 Vinternatt
 |
Under en vinternatt varierar temperaturen enligt funktionen
där \( y \;\, = \) temperaturen i grader Celsius och \( x \;\, = \) tiden i timmar efter midnatt Funktionen \(\, f(x)\):s definitionsmängd: \( \quad 0 \leq x \leq 8 \) a) Avgör algebraiskt om temperaturen är växande eller avtagande vid:
|
Påminnelse: En funktions definitionsmängd är mängden av alla \( \, x \, \) för vilka funktionen är definierad.
Copyright © 2021 TechPages AB. All Rights Reserved.
