Skillnad mellan versioner av "4.5 Absolutbelopp"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 46: | Rad 46: | ||
<td><math> \quad </math></td> | <td><math> \quad </math></td> | ||
<td> | <td> | ||
| − | |||
| − | |||
::<math> \left| \, \sqrt{3} \, \right| \, = \, \sqrt{3} </math> | ::<math> \left| \, \sqrt{3} \, \right| \, = \, \sqrt{3} </math> | ||
| + | |||
| + | ::<math> | \, a \, - \, b \, | \, = \, | \, b \, - \, a \, | </math> | ||
::<math> | \, i \, | \, = \, | \, \sqrt{-1} \, | \, = \, 1 \;\; \text{Varför?}</math> | ::<math> | \, i \, | \, = \, | \, \sqrt{-1} \, | \, = \, 1 \;\; \text{Varför?}</math> | ||
Versionen från 12 februari 2022 kl. 11.40
IND_VAL: v6 I, tis kl 11.15-12.20, sal 10. Övningar 4135-4141.
IND_VAL: v6 II, tor kl 14.40-15.50, sal 2. Övningar 4202-4211.
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
Repetition: Absolutbelopp för reella tal
De två raka strecken \( \; {\color{Red} |} \, \quad \, {\color{Red} |} \; \) kallas för absolutbelopp och betyder:
- Att göra om ett negativt tal till ett positivt tal
- och låta ett positivt tal vara oförändrat.
Ett tals absolutbelopp är talets positiva värde. Exempel:
|
\( \quad \) |
|
\( \quad \) |
|
Generellt gäller:
Absolutbeloppet \( \; | \, a - b \, | \; \) är avståndet mellan talen \( \, a \, \) och \( \, b \, \).
Det är irrelevant i vilken ordning talen skrivs. Det gäller: \( \quad | \, a - b \, | \, = \, | \, -(b - a) \, | \, = \, | \, b - a \, | \)
Ett specialfall av avståndet mellan två tal är, när det ena talet är \( \, 0 \, \):
Ett tals absolutbelopp = Talets avstånd från \( \, 0 \, \)
Om vi i den nya definitionen för avstånd \( \, | \, a - b \, | \, \) sätter in \( a = 0 \, \) och \( b = -5 \, \)
för att beräkna avståndet mellan \( 0 \, \) och \( -5 \, \) får vi:
- \[ | \, 0 - (-5) \, | \, = \, | \, 0 + 5 \, | \, = \, | \, 5 \, | \, = \, 5 \]
Och tar vi \( \, | \, b - a \, | \, \) blir det samma resultat:
- \[ | -5 - 0 \, | \, = \, | -5 \, | \, = \, 5 \]
\( 5 \, \) är alltså talet \( \, 5\):s och talet \( \, (-5)\):s avstånd från \( 0 \, \).
Detta ger oss en ny tolkning av absolutbeloppet som gäller för alla tal,
även för komplexa (se exemplet \( | \, i \, | = 1 \) ovan och motivera!):
Absolutbeloppet \( \; | \, a \, | \; \) är talet \( a\):s avstånd från 0.
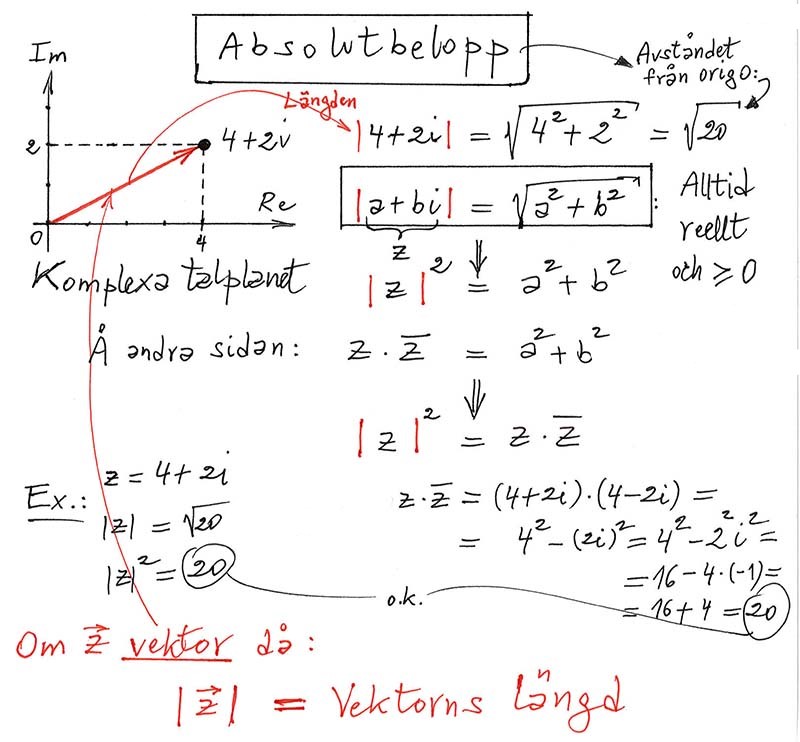
Absolutbelopp för komplexa tal
Copyright © 2022 TechPages AB. All Rights Reserved.