Skillnad mellan versioner av "4.5 Absolutbelopp"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (9 mellanliggande versioner av samma användare visas inte) | |||
| Rad 54: | Rad 54: | ||
<div class="ovnC"> | <div class="ovnC"> | ||
| − | |||
=== <b><span style="color:#931136">Allmän definition, funktion och graf</span></b> === | === <b><span style="color:#931136">Allmän definition, funktion och graf</span></b> === | ||
<div class="border-divblue"> | <div class="border-divblue"> | ||
| Rad 60: | Rad 59: | ||
<tr> | <tr> | ||
<td>Absolutbeloppet <math> \; | \, x \, | \; </math> av ett tal <math> x\, </math> definieras genom<span style="color:black">:</span> | <td>Absolutbeloppet <math> \; | \, x \, | \; </math> av ett tal <math> x\, </math> definieras genom<span style="color:black">:</span> | ||
| − | |||
::::<math> | \, x \, | \, = \, \begin{cases} \;\, x & \mbox{om } x \geq 0 \\ | ::::<math> | \, x \, | \, = \, \begin{cases} \;\, x & \mbox{om } x \geq 0 \\ | ||
| Rad 66: | Rad 64: | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
| − | |||
| − | |||
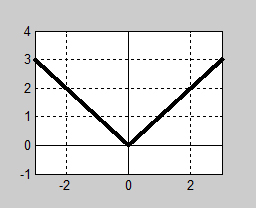
Grafen till <b><span style="color:#931136">funktionen <math> \; y = | \, x \, | \; </math></span></b> ser ut så här: | Grafen till <b><span style="color:#931136">funktionen <math> \; y = | \, x \, | \; </math></span></b> ser ut så här: | ||
| − | |||
</td> | </td> | ||
<td><math> \qquad </math></td> | <td><math> \qquad </math></td> | ||
| − | <td>[[Image: | + | <td>[[Image: Ovn_8_abs.jpg]]</td> |
</tr> | </tr> | ||
</table> | </table> | ||
| + | Absolutbeloppet är en funktion som är definierad och kontinuerlig för alla <math> x \, </math>. | ||
</div> | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</div> | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Rad 228: | Rad 163: | ||
</big></big> | </big></big> | ||
| + | |||
| + | [[Media: 4_5_Absolutbelopp_Ovn.pdf|<b><span style="color:blue">Övningar 4133-4141</span></b>]] | ||
<br> | <br> | ||
Nuvarande version från 11 mars 2025 kl. 13.37
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
Repetition: Absolutbelopp för reella tal
De två raka strecken \( \; {\color{Red} |} \, \quad \, {\color{Red} |} \; \) kallas för absolutbelopp och betyder:
- Att göra om ett negativt tal till ett positivt tal
- och låta ett positivt tal vara oförändrat.
Ett tals absolutbelopp är talets positiva värde. Exempel:
|
\( \quad \) |
|
\( \quad \) |
|
Allmän definition, funktion och graf
Absolutbeloppet är en funktion som är definierad och kontinuerlig för alla \( x \, \).
Användningar av absolutbelopp
Storheter som till sin natur är positiva. Ex.: avstånd, längd, area, volym,
massa (vikt), tid, lufttryck, vindstyrka, pengar, ålder, varaktighet, antal objekt, \( \, \ldots \; \).
Vi tittar närmare på avstånd:
Avstånd mellan två tal
Avståndet mellan \( \, 2 \, \) och \( \, 5 \, \) är differensen: \( \; 5 \, - \, 2 \, = \, 3 \;\; \) Ok!
Avståndet mellan \( -2 \) och \( -5 \) är differensen: \( -5 \, - \, (-2) \, = \, -5 \, + \, 2 \, = \, -3 \;\; \) Fel!
Avstånd kan inte vara negativt, måste vara positivt. Därför:
- \[ {\color{Red} |} \, -5 - (-2) \, { \color{Red} |} \; = \; { \color{Red} |} -5 + 2 \, { \color{Red} |} \, = \, { \color{Red} |} -3 \, { \color{Red} |} \; = \; 3 \]
Kastar vi om talens ordning blir det samma resultat:
- \[ { \color{Red} |} \, -2 - (-5) \, { \color{Red} |} \; = \; { \color{Red} |} -2 + 5 \, { \color{Red} |} \, = \, { \color{Red} |} \, 3 \, { \color{Red} |} \; = \; 3 \]
Generellt gäller:
Absolutbeloppet \( \; | \, a - b \, | \; \) är avståndet mellan talen \( \, a \, \) och \( \, b \, \).
Talens ordning är irrelevant: \( \; | \, a - b \, | \, = \, | \, -(b - a) \, | \, = \, | \, b - a \, | \)
Specialfall \( \; a \, = \, 0 \, \):
Ett tals absolutbelopp = Talets avstånd från \( \, 0 \, \)
Om vi i uttrycket för avstånd: \( \, | \, a - b \, | \, \) sätter in \( a = 0 \, \) och \( b = -5 \, \)
för att beräkna avståndet mellan \( 0 \, \) och \( -5 \, \) får vi:
- \[ | \, 0 - (-5) \, | \, = \, | \, 0 + 5 \, | \, = \, {\color{Red} {| \, 5 \, | \, = \, 5}} \]
Och tar vi \( \, | \, b - a \, | \, \) blir det samma resultat:
- \[ | -5 - 0 \, | \, = \, {\color{Red} {| -5 \, | \, = \, 5}} \]
\( 5 \, \) är alltså talet \( \, 5\):s och talet \( \, (-5)\):s avstånd från \( 0 \, \).
Detta ger oss en ny tolkning av absolutbeloppet som gäller för alla tal,
även för komplexa (se exemplet \( | \, i \, | = 1 \) ovan och motivera!):
Absolutbeloppet \( \; | \, a \, | \; \) är talet \( a\):s avstånd från 0.
Båda användningar av absolutbelopp: som avståndet från 0 och
som avståndet \( \, | \, a - b \, | \, \) mellan \( \, a \, \) och \( \, b \, \) kan tas över till komplexa tal:
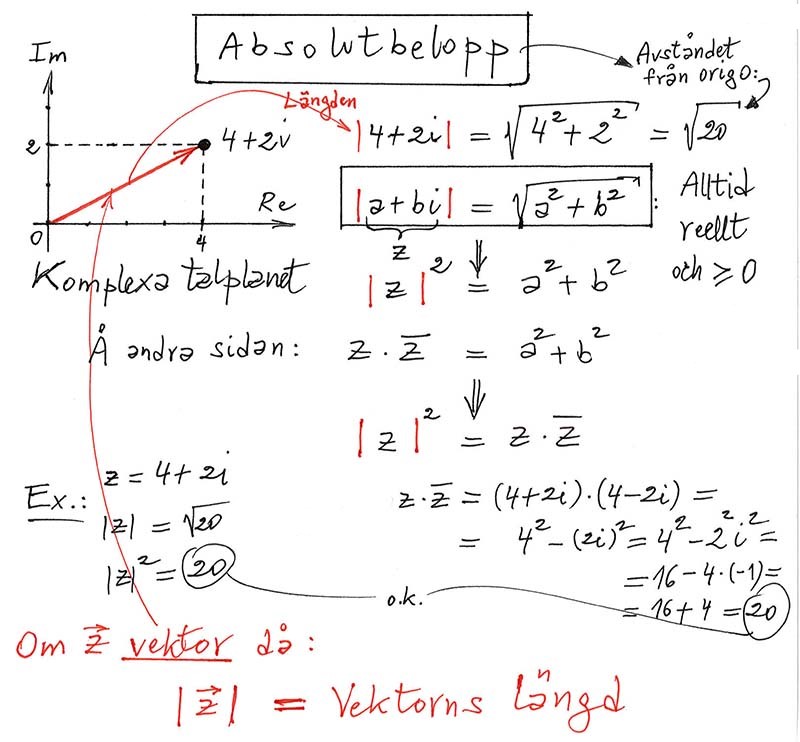
Absolutbelopp för komplexa tal
Allmän definition:
Absolutbelopp av ett komplext tal \( z \, = \, a + b\,i \;\; \) är \( \;\; | \, z \, | \; = \; \sqrt{a^2 + b^2} \; \)
Copyright © 2022 TechPages AB. All Rights Reserved.