4.6 Komplexa tal som vektorer
Från Mathonline
Version från den 11 februari 2025 kl. 22.13 av Taifun (Diskussion | bidrag)
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
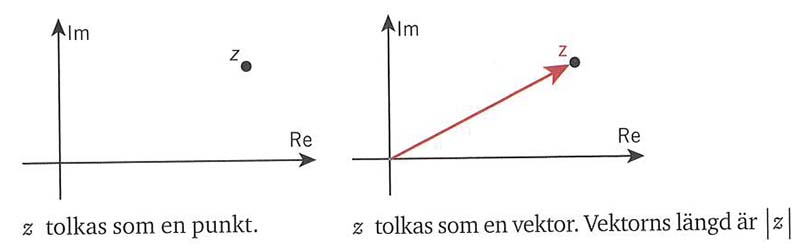
Punkt som vektor
Det komplexa talplanet
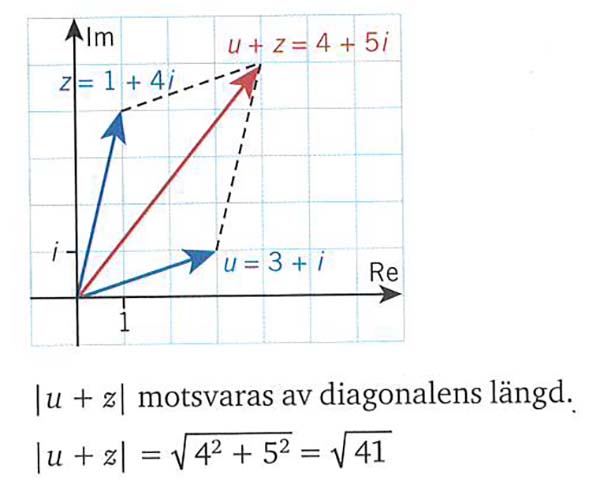
Addition av komplexa tal som addition av vektorer
Summan av två vektorer är:
Diagonalvektorn i det parallellogram som spänns upp av vektorerna
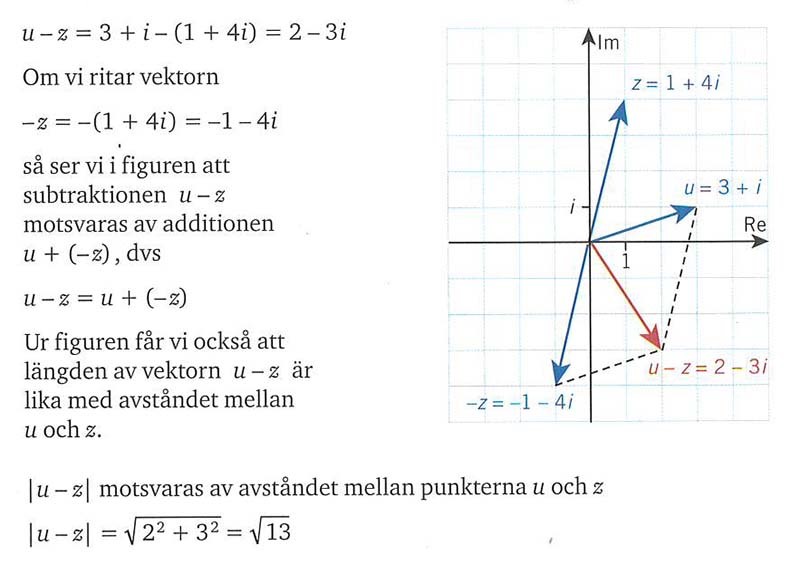
Subtraktion av komplexa tal som subtraktion av vektorer
u = 3 + i z = 1 + 4i
Differensen u - z bildas som summan u + (-z)
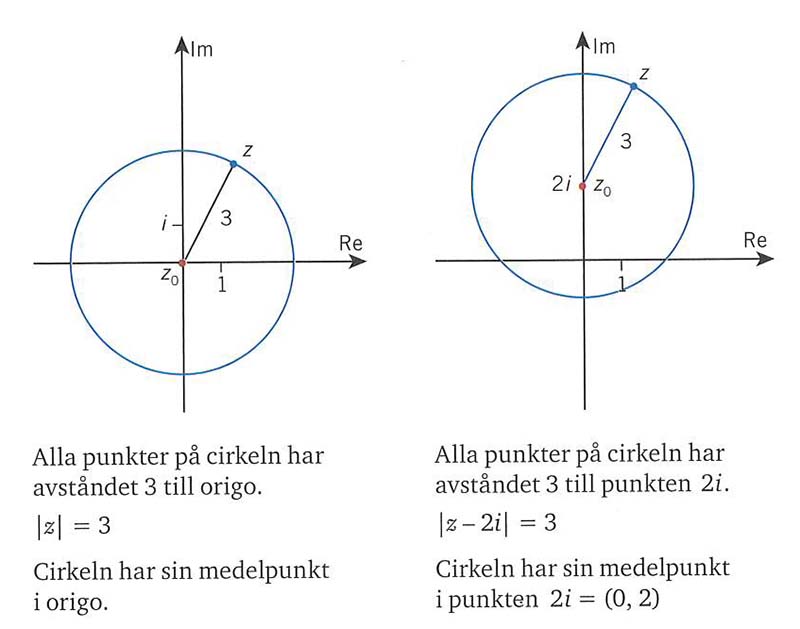
Cirkelns ekvation i det komplexa talplanet
Cirkel = Mängden av alla punkter \( \, z \, \) som har samma avstånd från medelpunkten \( \, z_0 \)
Avståndet mellan \( \, z \, \) och \( \, z_0 \; \) är \( \; | \, z - z_0 \, | \; \implies \; \)Cirkelns ekvation: \( \; | \, z - z_0 \, | \; = \; r\)
Två exempel:
Copyright © 2022 TechPages AB. All Rights Reserved.
