Skillnad mellan versioner av "4.6 Komplexa tal som vektorer"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (13 mellanliggande versioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
| − | + | __NOTOC__ | |
| − | + | ||
| − | + | ||
| − | + | ||
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
{{Not selected tab|[[4.5 Absolutbelopp| << Förra avsnitt]]}} | {{Not selected tab|[[4.5 Absolutbelopp| << Förra avsnitt]]}} | ||
| − | {{Selected tab|[[4.6 Komplexa tal som vektorer|Genomgång]]}} | + | {{Selected tab|[[4.6 Komplexa tal som vektorer|<span style="font-weight:lighter">Genomgång</span>]]}} |
{{Not selected tab|[[Media: 4_6_Komplexa_vektorer_Ovn.pdf|Övningar]]}} | {{Not selected tab|[[Media: 4_6_Komplexa_vektorer_Ovn.pdf|Övningar]]}} | ||
{{Not selected tab|[[Media: 4_6_Komplexa_vektorer_Facit.pdf|Facit]]}} | {{Not selected tab|[[Media: 4_6_Komplexa_vektorer_Facit.pdf|Facit]]}} | ||
| Rad 16: | Rad 13: | ||
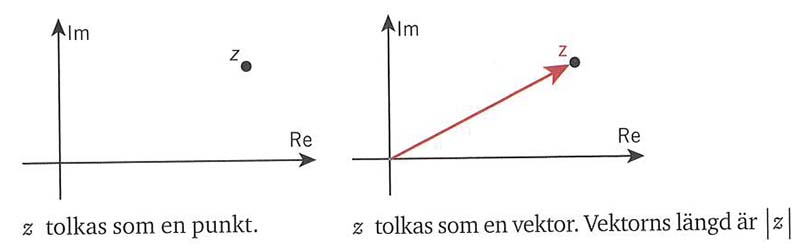
= <b><span style="color:#931136">Punkt som vektor</span></b> = | = <b><span style="color:#931136">Punkt som vektor</span></b> = | ||
<div class="ovnE"> | <div class="ovnE"> | ||
| − | === | + | === <span style="color:#931136">Det komplexa talplanet</span> === |
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_6_Komplexa_vektorer_1.jpg]] | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_6_Komplexa_vektorer_1.jpg]] | ||
</div> | </div> | ||
| Rad 24: | Rad 21: | ||
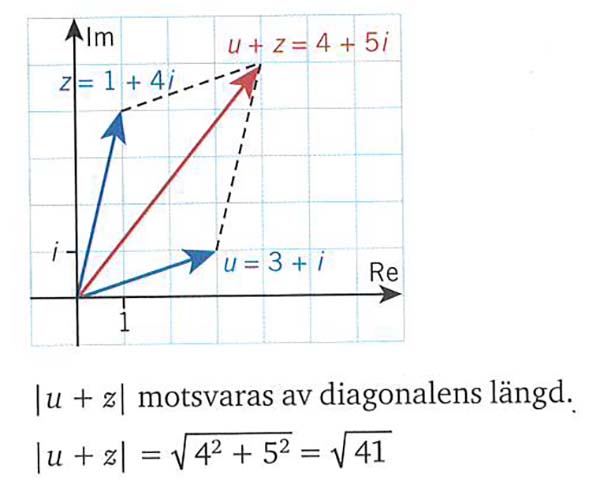
= <b><span style="color:#931136">Addition av komplexa tal som addition av vektorer</span></b> = | = <b><span style="color:#931136">Addition av komplexa tal som addition av vektorer</span></b> = | ||
<div class="ovnC"> | <div class="ovnC"> | ||
| − | === | + | === <span style="color:#931136">Summan av två vektorer u och z är vektorn som bildas av:</span> === |
| + | === <span style="color:#931136">Diagonalen i det parallellogram som spänns upp av vektorerna</span> === | ||
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_6_Komplexa_vektorer_2.jpg]] | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_6_Komplexa_vektorer_2.jpg]] | ||
</div> | </div> | ||
| Rad 32: | Rad 30: | ||
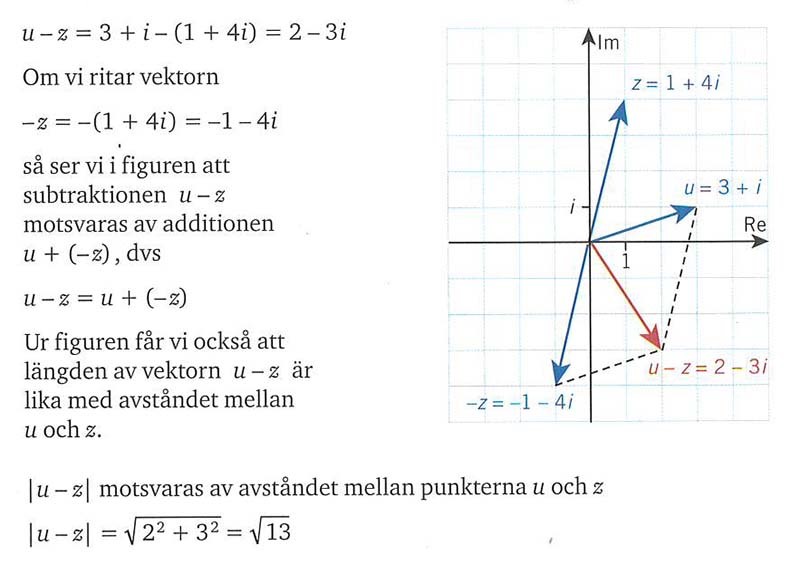
= <b><span style="color:#931136">Subtraktion av komplexa tal som subtraktion av vektorer</span></b> = | = <b><span style="color:#931136">Subtraktion av komplexa tal som subtraktion av vektorer</span></b> = | ||
<div class="ovnA"> | <div class="ovnA"> | ||
| − | === | + | === <span style="color:#931136"> u = 3 + i z = 1 + 4i</span> === |
| − | === | + | === <span style="color:#931136">Differensen u - z bildas som summan u + (-z)</span> === |
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_6_Komplexa_vektorer_3a.jpg]] | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_6_Komplexa_vektorer_3a.jpg]] | ||
</div> | </div> | ||
| Rad 39: | Rad 37: | ||
| − | = <b><span style="color:#931136">Cirkelns ekvation</span></b> = | + | = <b><span style="color:#931136">Cirkelns ekvation i det komplexa talplanet</span></b> = |
<div class="ovnE"> | <div class="ovnE"> | ||
| − | === | + | === <span style="color:#931136">Cirkel = Mängden av alla punkter <math> \, z \, </math> som har samma avstånd från</span> medelpunkten <math> \, z_0 </math> === |
| − | === | + | === <span style="color:#931136">[[4.5_Absolutbelopp#Avst.C3.A5nd_mellan_tv.C3.A5_tal|<span style="color:blue">Avståndet</span>]] mellan <math> \, z \, </math> och <math> \, z_0 \; </math> är <math> \; | \, z - z_0 \, | \; \implies \; </math></span>Cirkelns ekvation<span>:</span> <math> \; | \, z - z_0 \, | \; = \; r</math> === |
| − | === | + | === <span style="color:#931136">Två exempel:</span> === |
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_6_Komplexa_vektorer_4.jpg]] | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_6_Komplexa_vektorer_4.jpg]] | ||
</div> | </div> | ||
</div> | </div> | ||
| + | |||
| + | [[Media: 4_2_Komplexa tal2_Ovn.pdf|<b><span style="color:blue">Övningar 4202-4207</span></b>]] | ||
<br> | <br> | ||
| Rad 59: | Rad 59: | ||
| − | [[Matte:Copyrights|Copyright]] © | + | [[Matte:Copyrights|Copyright]] © 2025 <b><span style="color:blue">Lieta AB</span></b>. All Rights Reserved. |
Nuvarande version från 13 november 2025 kl. 08.10
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
Punkt som vektor
Addition av komplexa tal som addition av vektorer
Summan av två vektorer u och z är vektorn som bildas av:
Diagonalen i det parallellogram som spänns upp av vektorerna
Subtraktion av komplexa tal som subtraktion av vektorer
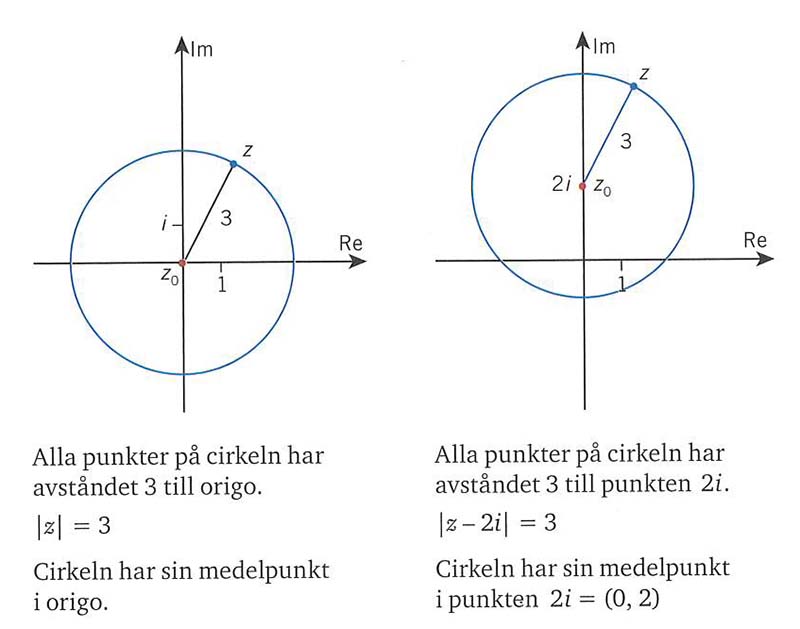
Cirkelns ekvation i det komplexa talplanet
Cirkel = Mängden av alla punkter \( \, z \, \) som har samma avstånd från medelpunkten \( \, z_0 \)
Avståndet mellan \( \, z \, \) och \( \, z_0 \; \) är \( \; | \, z - z_0 \, | \; \implies \; \)Cirkelns ekvation: \( \; | \, z - z_0 \, | \; = \; r\)
Två exempel:
Copyright © 2025 Lieta AB. All Rights Reserved.