Skillnad mellan versioner av "4.8 Komplexa tal på polär form"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 3: | Rad 3: | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
{{Not selected tab|[[4.7 Visualiseringar i det komplexa talplanet| << Förra avsnitt]]}} | {{Not selected tab|[[4.7 Visualiseringar i det komplexa talplanet| << Förra avsnitt]]}} | ||
| − | {{Selected tab|[[4.8 Komplexa tal på polär form|Genomgång]]}} | + | {{Selected tab|[[4.8 Komplexa tal på polär form|<span style="font-weight:lighter">Genomgång</span>]]}} |
{{Not selected tab|[[Media: 4_8 Komplexa_polar_Ovn.pdf|Övningar]]}} | {{Not selected tab|[[Media: 4_8 Komplexa_polar_Ovn.pdf|Övningar]]}} | ||
{{Not selected tab|[[Media: 4_8 Komplexa_polar_Facit.pdf|Facit]]}} | {{Not selected tab|[[Media: 4_8 Komplexa_polar_Facit.pdf|Facit]]}} | ||
Nuvarande version från 12 november 2025 kl. 13.43
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
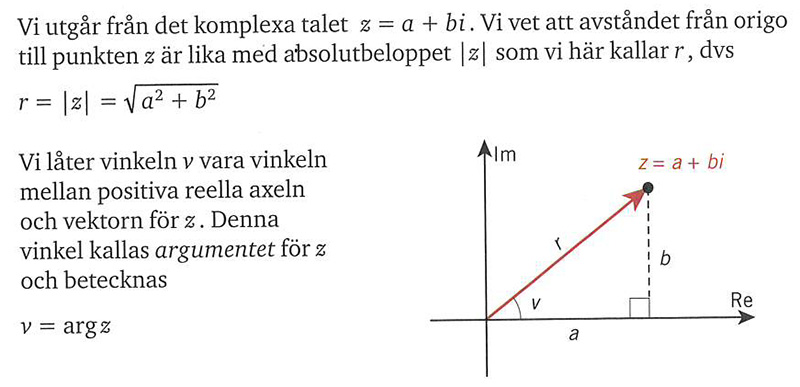
Argumentet för ett komplext tal z
Polära koordinater (r, v)
Copyright © 2022 TechPages AB. All Rights Reserved.