Skillnad mellan versioner av "4.8 Komplexa tal på polär form"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 13: | Rad 13: | ||
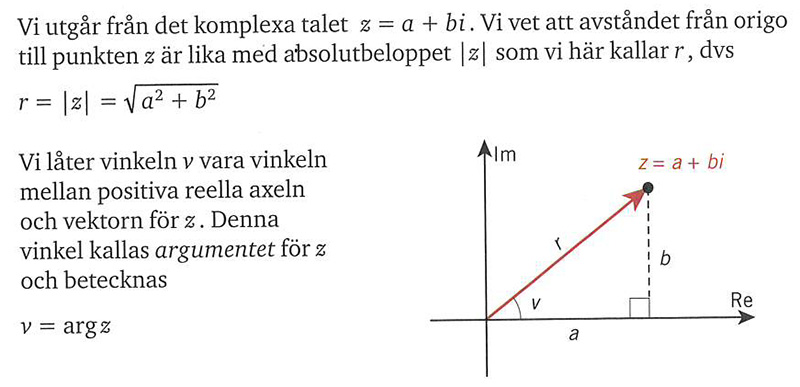
= <b><span style="color:#931136">Argumentet för ett komplext tal z</span></b> = | = <b><span style="color:#931136">Argumentet för ett komplext tal z</span></b> = | ||
<div class="ovnE"> | <div class="ovnE"> | ||
| − | === | + | === <span style="color:#931136">Vinkeln v = arg z</span> === |
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_8_Komplexa_Polar_1.jpg]] | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_8_Komplexa_Polar_1.jpg]] | ||
</div> | </div> | ||
| − | === | + | === <span style="color:#931136"> <math> \tan v \, = \, b/a \; \implies \; v \, = \, \tan^{(-1)} (b/a) </math></span> === |
</div> | </div> | ||
| Rad 22: | Rad 22: | ||
= <b><span style="color:#931136">Polära koordinater (r, v)</span></b> = | = <b><span style="color:#931136">Polära koordinater (r, v)</span></b> = | ||
<div class="ovnC"> | <div class="ovnC"> | ||
| − | === | + | === <span style="color:#931136">Vektorns längd r = Avstånd från Origo</span> === |
| − | === | + | === <span style="color:#931136">Vinkeln v = Argumentet för z (se figuren ovan)</span> === |
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_8_Komplexa_Polar_2.jpg]] | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_8_Komplexa_Polar_2.jpg]] | ||
</div> | </div> | ||
Versionen från 12 november 2025 kl. 13.42
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
Argumentet för ett komplext tal z
Vinkeln v = arg z
\( \tan v \, = \, b/a \; \implies \; v \, = \, \tan^{(-1)} (b/a) \)
Polära koordinater (r, v)
Vektorns längd r = Avstånd från Origo
Vinkeln v = Argumentet för z (se figuren ovan)
Copyright © 2022 TechPages AB. All Rights Reserved.
