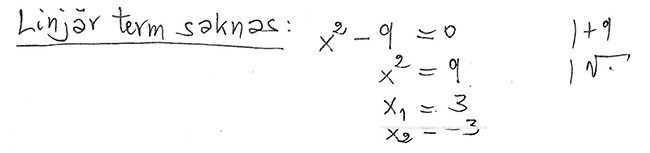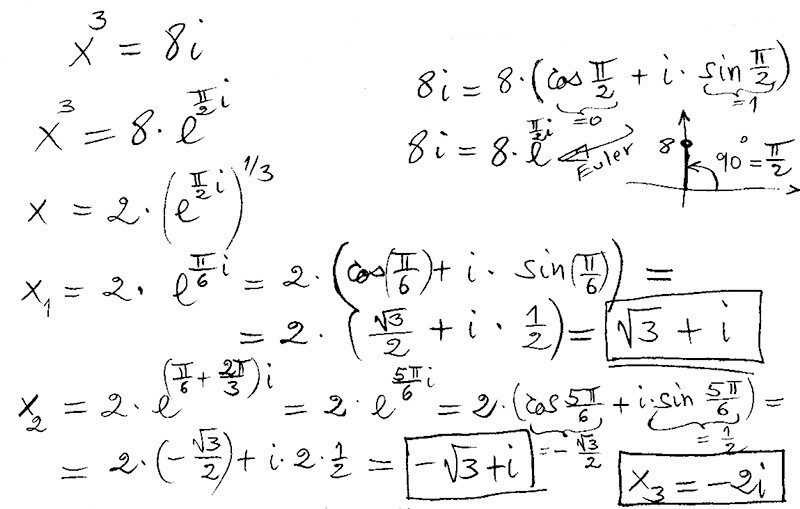Skillnad mellan versioner av "4.14 Polynomekvationer"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (8 mellanliggande versioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
__NOTOC__ | __NOTOC__ | ||
| − | |||
| − | |||
| − | |||
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
| Rad 25: | Rad 22: | ||
<big> | <big> | ||
<div class="border-divblue"> | <div class="border-divblue"> | ||
| − | Om 2:gradsekvationen <math> \; x^2 + p\,x + q \; = \; 0 \; </math> har | + | Om 2:gradsekvationen <math> \; x^2 + p\,x + q \; = \; 0 \; </math> har lösningarna |
| − | + | <math> x_1\, </math> och <math> x_2\, </math> så gäller<span style="color:black">:</span> <math> \qquad \boxed{\begin{align} x_1 + x_2 & = -p \\ | |
x_1 \cdot x_2 & = q | x_1 \cdot x_2 & = q | ||
\end{align}} </math> | \end{align}} </math> | ||
| Rad 34: | Rad 31: | ||
| − | = <b><span style="color:#931136"> | + | = <b><span style="color:#931136">Den konstanta termen saknas: Nollproduktmetoden</span></b> = |
| − | <div class=" | + | <div class="ovnE"> |
| − | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: | + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 3_3_Nollproduktmetoden.jpg]] </div> |
</div> | </div> | ||
| + | |||
| + | |||
| + | = <b><span style="color:#931136">Den linjära termen saknas: Kvadratrotsmetoden</span></b> = | ||
| + | <div class="ovnE"> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 3_3_Kvadratrotsmetodena.jpg]] </div> | ||
</div> | </div> | ||
| Rad 47: | Rad 49: | ||
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_14_Polynomekv_2.jpg]]</div> | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_14_Polynomekv_2.jpg]]</div> | ||
| + | </div> | ||
| − | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: | + | = <b><span style="color:#931136">Att dra (3:e) roten ur ett komplext tal: Använd Euler</span></b> = |
| + | <div class="ovnE"> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_14_Polynomekv_3a.jpg]]</div> | ||
</div> | </div> | ||
| + | |||
| + | |||
| + | = <b><span style="color:#931136">Repetition: Konjugatets egenskaper</span></b> = | ||
| + | <div class="ovnC"> | ||
| + | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_2_Komplexa_tal_2.jpg]] | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | |||
| + | [[Media: 4_14_Polynomekv_Ovn.pdf|<b><span style="color:blue">Övningar 4403-4415</span></b>]] | ||
Nuvarande version från 27 mars 2025 kl. 09.37
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
Orientering om andragradsekvationer
Vietas formler
Om 2:gradsekvationen \( \; x^2 + p\,x + q \; = \; 0 \; \) har lösningarna
\( x_1\, \) och \( x_2\, \) så gäller: \( \qquad \boxed{\begin{align} x_1 + x_2 & = -p \\ x_1 \cdot x_2 & = q \end{align}} \)
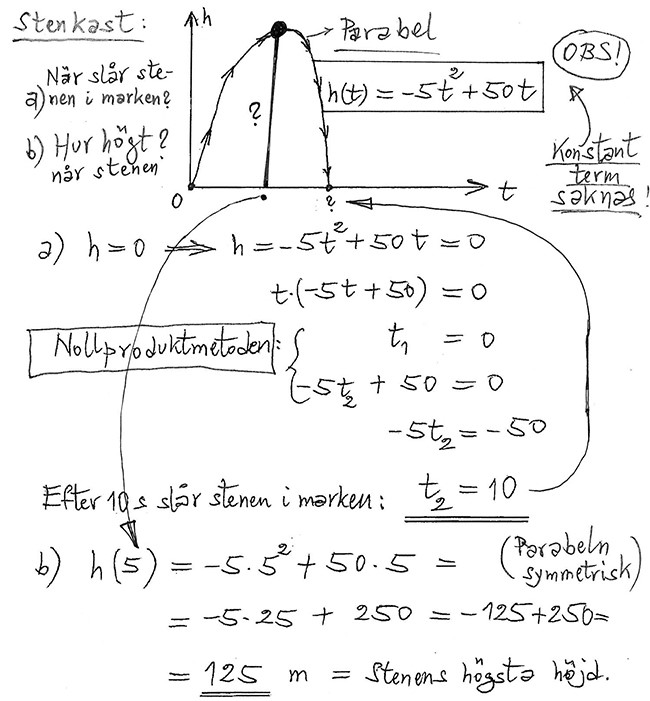
Den konstanta termen saknas: Nollproduktmetoden
Den linjära termen saknas: Kvadratrotsmetoden
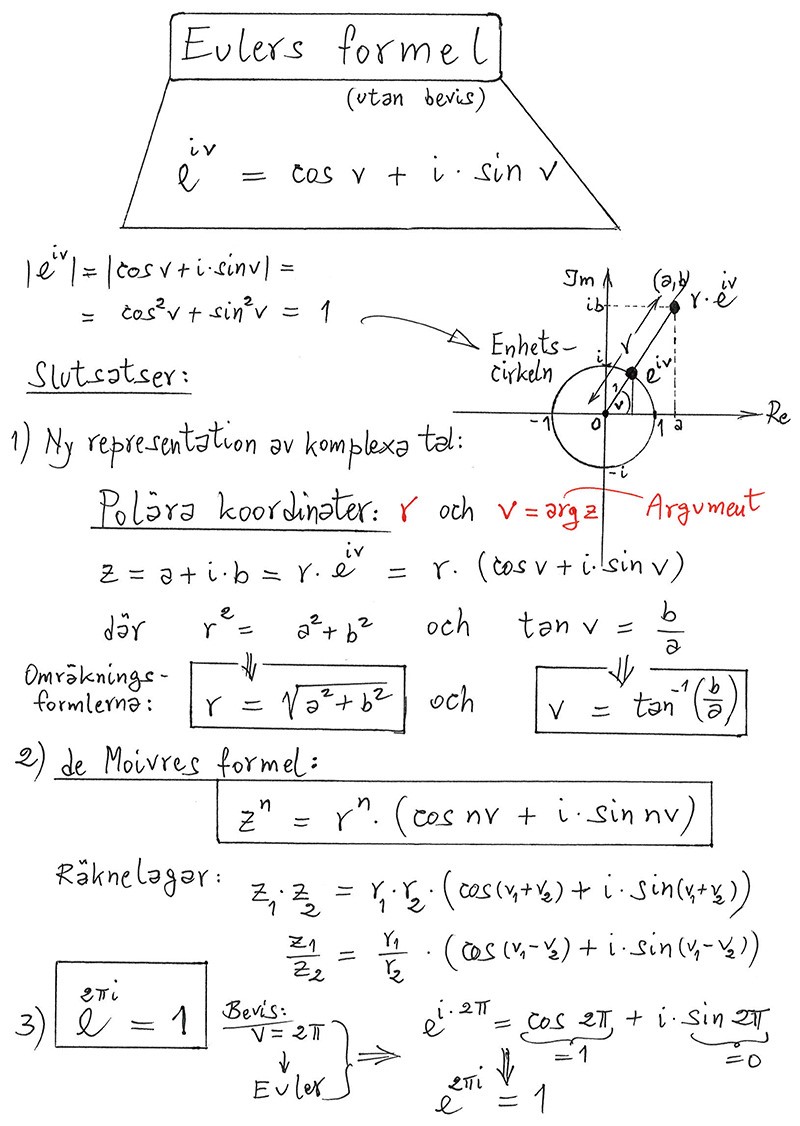
Användning av Eulers formel
Att dra (3:e) roten ur ett komplext tal: Använd Euler
Repetition: Konjugatets egenskaper
Copyright © 2022 TechPages AB. All Rights Reserved.