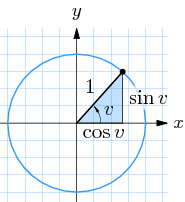Repetition Trigonometri

Innehållsförteckning

1.1 Rätvinkliga trianglar

Övningar

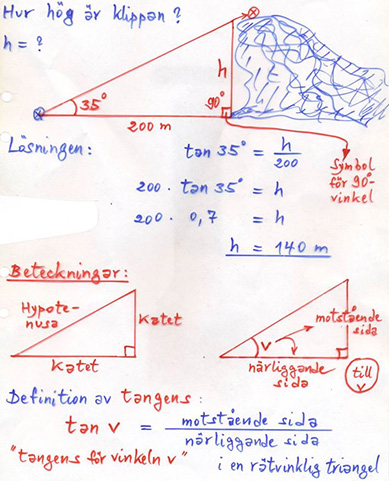
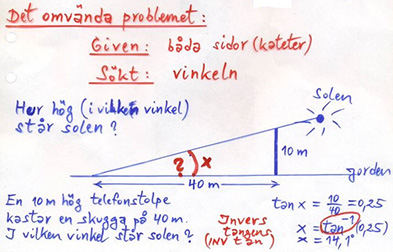
1.2 Godtyckliga trianglar          1.3 Trigon. identiteter  >>       Trigon = Triangel på latin. \( \qquad\qquad\qquad\qquad\quad \) Trigonometri = Att mäta trianglar. 1.1 Trigonometri i rätvinkliga trianglar Tangens för \( \, v \, < \, 90^\circ \) Se även längre ned. 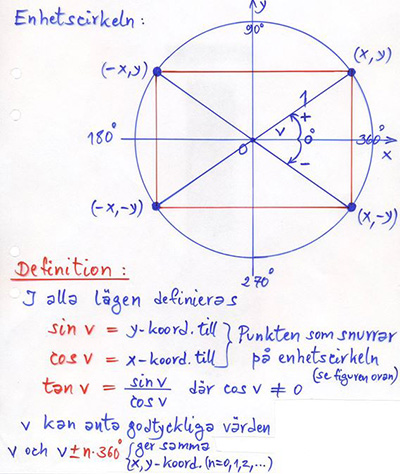Sinus och Cosinus för \( \, v \, < \, 90^\circ \)    1.2 Trigonometri i godtyckliga trianglar        <<  Förra avsnitt: Genomgång rätvinkliga          Formelsamling Trigonometri          Nästa avsnitt  >>       Enhetscirkeln är cirkeln med radien \( \, r \, = \, 1 \, \) och medelpunkten \( \, M \, = \, O \, \) (origo). Om en punkt \( \, P\,(x, y) \, \) snurrar på enhetscirkeln och \( \, v \, \) är vinkeln mellan \( \, x\)-axeln och \( \, \overline{OP} \), så gäller: \( \qquad\qquad\quad \) \(\begin{array}{rcl} x & = & \cos v \\ y & = & \sin v \end{array}\) I cirklar med radien \( \, r \, > \, 1 \, \) förblir vinkeln \( \, v \, \) den samma och därmed \( \, \cos v = (r \cdot x) / r = x \, \) och \( \, \sin v = (r \cdot y) / r = y \), precis som ovan. Dvs formlerna för \( \, x = \cos v \, \) och \( \, y = \sin v \, \) stämmer fortfarande, även om \( \, r \, > \, 1 \, \). De här formlerna används för att definiera de trigonometriska funktionerna i godtyckliga trianglar, dvs för vinklar \( \, v \, \geq \, 90^\circ \, \). 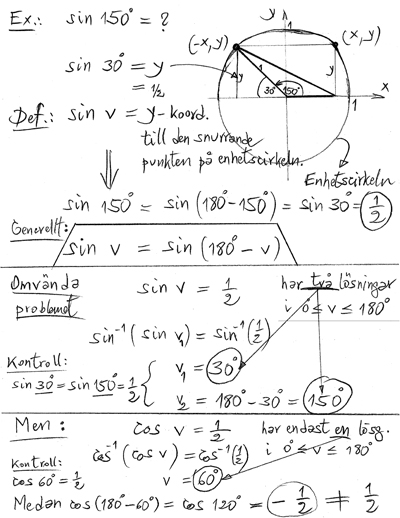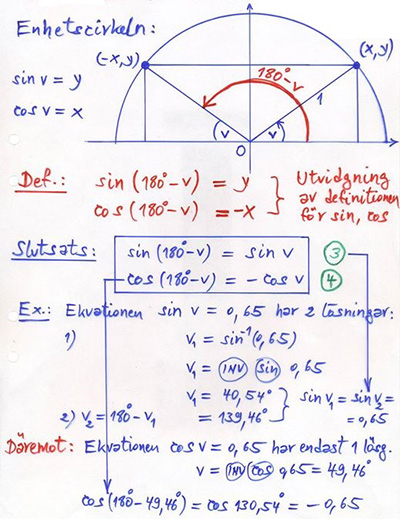Sinus och Cosinus för vinklar i intervallet: \( \quad 90^\circ \, \leq \, v \, \leq \, 180^\circ \) Exempel: \[ \sin 150^\circ \, = \, \sin (180^\circ - 30^\circ) \, = \, \sin 30^\circ \, = \, 1 / 2 \] \[ \cos 120^\circ \, = \, \cos (180^\circ - 60^\circ) \, = \, -\cos 60^\circ \, = \, -(1 / 2) \] Förklaring med enhetscirkeln: Punkten till vinkeln \( \, v \, \) har samma \( \, y\)-koordinat (\(=\sin v\)) som punkten till vinkeln \( \, 180-v \). Punkten till vinkeln \( \, v \, \) har samma \( \, x\)-koordinat (\(=\cos v\)) som punkten till vinkeln \( \, 180-v \, \) med omvänt tecken.    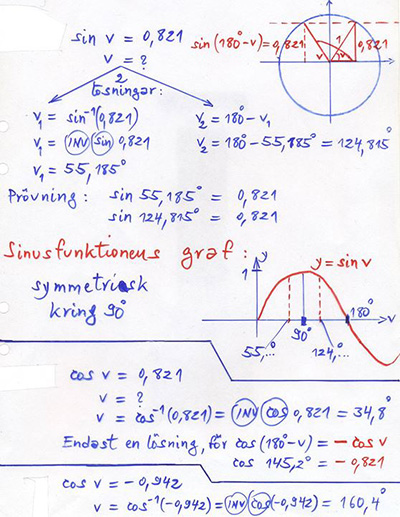Ekvationer           med    Sin & Cos: Sinus, Cosinus och Tangens för alla vinklar   En gång till      Sin & Cos   för \( v \geq 90^\circ \)    i trianglar: Slutsatser En sinusekvation har i intervallet \( \, 0^\circ \leq v \leq 180^\circ \, \) alltid två lösningar. En cosinusekvation har i intervallet \( \, 0^\circ \leq v \leq 180^\circ \, \) endast en lösning. Copyright © 2021 TechPages AB. All Rights Reserved.