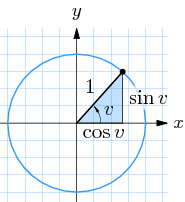Skillnad mellan versioner av "Repetition Trigonometri"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 7: | Rad 7: | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| + | |||
<big> | <big> | ||
| − | + | == <b><span style="color:#931136">Trigonometri i rätvinkliga trianglar</span></b> == | |
| − | == <b><span style="color:#931136">Trigonometri i rätvinkliga trianglar | + | |
<br> | <br> | ||
<big><b><span style="color:#931136">Tangens för <math> \, v \, < \, 90^\circ </math></span></b></big> | <big><b><span style="color:#931136">Tangens för <math> \, v \, < \, 90^\circ </math></span></b></big> | ||
| Rad 39: | Rad 39: | ||
<div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 5 SinusCosinus_55.jpg]] </div> | <div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 5 SinusCosinus_55.jpg]] </div> | ||
| − | |||
| − | == <b><span style="color:#931136">Godtyckliga trianglar | + | == <b><span style="color:#931136">Godtyckliga trianglar</span></b> == |
<big><b><span style="color:#931136">Enhetscirkeln</span></b></big> | <big><b><span style="color:#931136">Enhetscirkeln</span></b></big> | ||
Versionen från 15 augusti 2021 kl. 13.10
| Innehållsförteckning | Kursens presentation | Formelsamling Trigonometri |
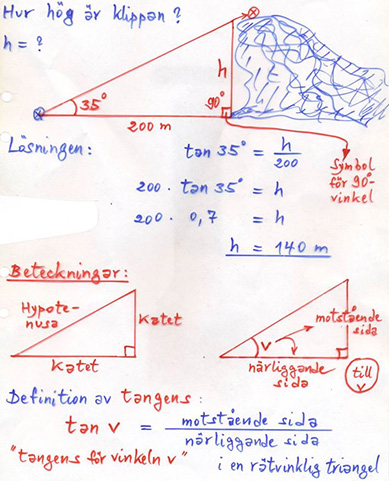
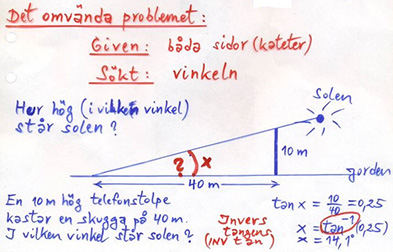
Trigonometri i rätvinkliga trianglar
Tangens för \( \, v \, < \, 90^\circ \)
|
|
|
Sinus och Cosinus för \( \, v \, < \, 90^\circ \)
Godtyckliga trianglar
Enhetscirkeln
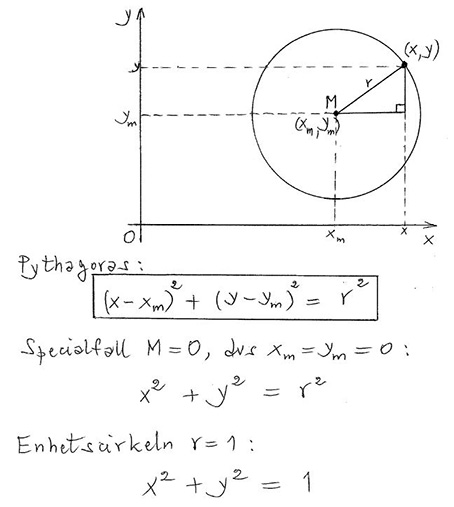
Cirkel \( \, = \, \) Mängden av alla punkter som har samma avstånd (radien \( \, r \, \)) från en punkt (medelpunkten \( \, M \, \)).
Cirkelns ekvation:
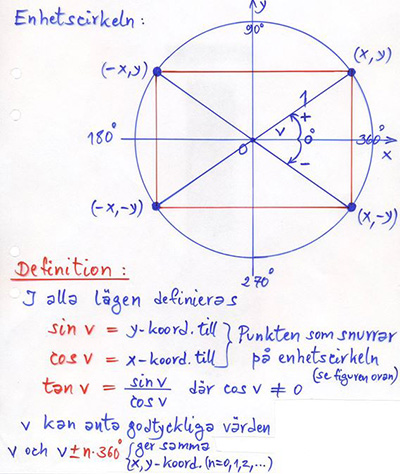
Enhetscirkeln är cirkeln med radien \( \, r \, = \, 1 \, \) och medelpunkten \( \, M \, = \, O \, \) (origo).
Om en punkt \( \, P\,(x, y) \, \) snurrar på enhetscirkeln och \( \, v \, \) är vinkeln mellan \( \, x\)-axeln och \( \, \overline{OP} \), så gäller:
| \( \qquad\qquad\quad \) |
\(\begin{array}{rcl} x & = & \cos v \\
y & = & \sin v
\end{array}\)
|
I cirklar med radien \( \, r \, > \, 1 \, \) förblir vinkeln \( \, v \, \) den samma och därmed \( \, \cos v = \displaystyle \frac{r \cdot \; x}{r} = x \, \) och \( \, \sin v = \displaystyle \frac{r \cdot \; y}{r} = y \), precis som ovan.
Detta används för att definiera de trigonometriska funktionerna i godtyckliga trianglar, dvs för vinklar \( \, v \, \geq \, 90^\circ \, \).
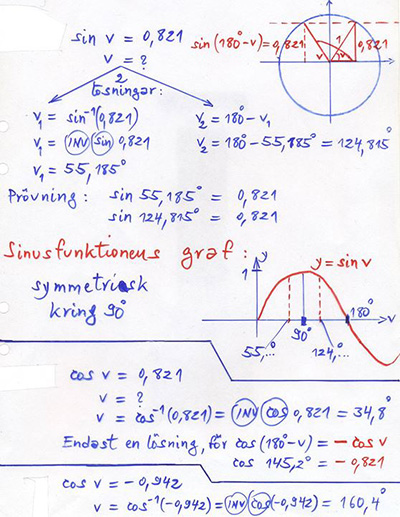
Sinus och Cosinus för vinklar i intervallet: \( \quad 90^\circ \, \leq \, v \, \leq \, 180^\circ \)
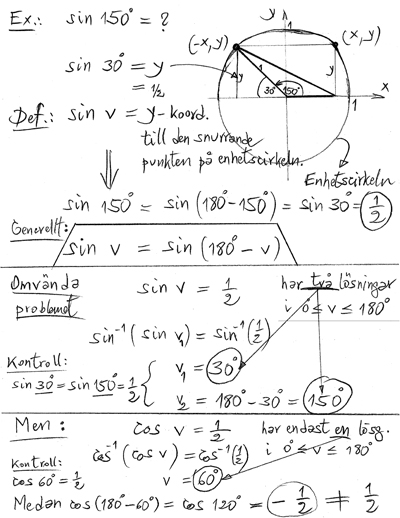
Exempel:
- \[ \sin 150^\circ \, = \, \sin (180^\circ - 30^\circ) \, = \, \sin 30^\circ \, = \, \frac{1}{2} \]
- \[ \cos 120^\circ \, = \, \cos (180^\circ - 60^\circ) \, = \, -\cos 60^\circ \, = \, -\frac{1}{2} \]
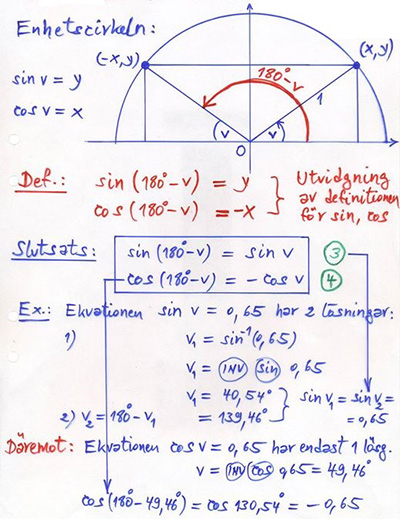
Förklaring med enhetscirkeln:
Punkten till vinkeln \( \, v \, \) har samma \( \, y\)-koordinat (\(=\sin v\)) som punkten till vinkeln \( \, 180-v \).
Punkten till vinkeln \( \, v \, \) har samma \( \, x\)-koordinat (\(=\cos v\)) som punkten till vinkeln \( \, 180-v \, \) med omvänt tecken.
| Ekvationer
med Sin & Cos:
|
Sinus, Cosinus och Tangens för alla vinklar
|
|
En gång till
Sin & Cos för \( v \geq 90^\circ \) i trianglar:
|
|
En cosinusekvation har i intervallet \( \, 0^\circ \leq v \leq 180^\circ \, \) endast en lösning.
Copyright © 2021 TechPages AB. All Rights Reserved.