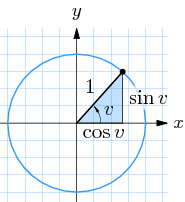Skillnad mellan versioner av "Repetition Trigonometri"

Från Mathonline
Hoppa till: navigering, sök
m
m
 
(128 mellanliggande versioner av samma användare visas inte)
Rad 3: Rad 3:
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
{{Not selected tab|[[Matte 4 Innehållsförteckning|Innehållsförteckning]]}}
 
{{Not selected tab|[[Matte 4 Innehållsförteckning|Innehållsförteckning]]}}
−
{{Selected tab|[[Huvudsida|Kursens presentation]]}}
+
{{Selected tab|[[Repetition Trigonometri|1.1 Rätvinkliga trianglar]]}}
−
{{Not selected tab|[[Media: Formelsamling Matte 4.pdf|Formelsamling Trigonometri]]}}
+
{{Not selected tab|[[Övningar till Repetition Trigonometri|Övningar]]}}
 +
<!-- {{Not selected tab|[[Formelsamling Matte 4 Trigonometri|Formelsamling Trigonometri]]}} -->
 +
{{Selected tab|[[Repetition_Trigonometri#1.2_Trigonometri_i_godtyckliga_trianglar|1.2 Godtyckliga trianglar]]}}
 +
{{Not selected tab|[[1.3_Trigonometriska_identiteter|1.3 Trigon. identiteter&nbsp;&nbsp;>> ]]}}
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
 +
  
 
<big>
 
<big>
−
<br>
+
=== <span style="color:#931136"><i>Trigon</i> = Triangel på latin. <math> \qquad\qquad\qquad\qquad\quad </math> <i>Trigonometri</i> = Att mäta trianglar.</span> ===
−
Detta kapitels övningar finns inte på webben (pga tidsbrist). Därför:
+
  
−
Läs igenom genomgångarna här, men använd för övningarna boken <i>Matematik 5000</i>.
 
  
−
== <b><span style="color:#931136">Utdrag ur planeringen:</span></b> ==
+
== <b><span style="color:#931136">1.1 Trigonometri i rätvinkliga trianglar</span></b> ==
−
<br>
+
−
<div style="border:1px solid black;display:inline-table;margin-left: 30px;"> [[Image: Planering_Integr_Rubrik_2019_800a.jpg]] </div>
+
−
<div style="border:1px solid black;display:inline-table;margin-left: 30px;"> [[Image: Planering_Trigonometri_2019_800b.jpg]] </div>
+
−
<br>
+
−
== <b><span style="color:#931136">5.1 Trigonometri i rätvinkliga trianglar <math> \qquad\;\; </math> <small><small>Övningar: &nbsp; Boken, sid 208</small></small></span></b> ==
+
−
<br>
+
 
<big><b><span style="color:#931136">Tangens för <math> \, v \, < \, 90^\circ </math></span></b></big>
 
<big><b><span style="color:#931136">Tangens för <math> \, v \, < \, 90^\circ </math></span></b></big>
 
<table>
 
<table>
 
<tr>
 
<tr>
−
   <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 1 Tangens_55.jpg]] </div>
+
   <td>
  
 +
<div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 1 Tangens_55.jpg]] </div>
 +
 +
Se även [[Repetition_Trigonometri#Sinus.2C_Cosinus_och_Tangens_f.C3.B6r_alla_vinklar|<b><span style="color:blue">längre ned</span></b>]].
 +
 +
 +
<big><b><span style="color:#931136">Sinus och Cosinus för <math> \, v \, < \, 90^\circ </math></span></b></big>
 +
 +
<div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 5 SinusCosinus_55.jpg]] </div>
  
−
<div class="ovnA">
 
−
<big>{{#NAVCONTENT:Flera exempel på tangens|Exempel på tangens}}</big>
 
−
</div>
 
 
</td>
 
</td>
 
   <td><div style="border:1px solid black;display:inline-table;margin-left: 20px;"> [[Image: 2 Tangensproblemet_55.jpg]] </div>
 
   <td><div style="border:1px solid black;display:inline-table;margin-left: 20px;"> [[Image: 2 Tangensproblemet_55.jpg]] </div>
  
  
 +
&nbsp;&nbsp;<div style="border:1px solid black;display:inline-table;margin-left: 12px;"> [[Image: 3 OmvantProblem_55.jpg]] </div>
  
  
  
−
&nbsp;&nbsp;<div style="border:1px solid black;display:inline-table;margin-left: 12px;"> [[Image: 3 OmvantProblem_55.jpg]] </div>
 
−
</td>
 
−
</tr>
 
−
</table>
 
  
  
−
<big><b><span style="color:#931136">Sinus och Cosinus för <math> \, v \, < \, 90^\circ </math></span></b></big>
 
  
−
<div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 5 SinusCosinus_55.jpg]] </div>
 
−
<br>
 
−
== <b><span style="color:#931136">5.2 Exakta trigonometriska värden / Enhetscirkeln <math> \;\; </math> <small><small>Övningar: &nbsp; Boken, sid 209 / 210</small></small></span></b> ==
 
−
<br>
 
−
<big><b><span style="color:#931136">Två speciella vinklar<span style="color:black">:</span> <math> \, 45^\circ \, </math> och <math> \, 60^\circ \, </math> </span></b></big>
 
  
−
Pythagoras satsen används på halva kvadraten med sidan <math> \, 1 \, </math> för att få diagonalen <math> \, \sqrt{2} </math>. Sedan bestäms <math> \, \sin 45^\circ \, </math> och <math> \, \tan 45^\circ </math><span style="color:black">:</span>
 
  
−
<div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 6_Exakta_trig_varden_45_60.jpg]] </div>
 
  
−
På liknande sätt används Pythagoras på halva liksidiga triangeln med sidan <math> \, 2 \, </math> för att få höjden <math> \, \sqrt{3} </math>. Sedan bestäms <math> \, \sin 60^\circ </math> och <math> \, \cos 60^\circ </math>.
 
  
−
"Exakt" betyder: Gå inte över till decimaltal, dvs:
 
  
−
::* &nbsp;&nbsp; Bibehåll bråk med endast heltal i täljare och nämnare,
 
−
::* &nbsp;&nbsp; Bibehåll rötter som inte ger heltal.
 
  
−
En konsekvens blir att inte ens rötter ska stå kvar i bråkens nämnare. Ta upp dem genom förlängning med <math> \, \sqrt{{\color{White} {\cdots}}}  </math>, t.ex.<span style="color:black">:</span>
 
  
−
::<math> \displaystyle \frac{1}{\sqrt{2}} \, = \, \frac{1 \, \cdot \, {\color{Red} {\sqrt{2}}}}{\sqrt{2} \cdot {\color{Red} {\sqrt{2}}}} \, = \, \frac{\sqrt{2}}{2} \, = \, \frac{1}{2} \, \sqrt{2} </math>
 
  
−
                             
 
−
<big><b><span style="color:#931136">Ytterligare exakta trigonometriska värden </span></b></big>
 
  
−
Andra geometriska satser ger följande exakta värden<span style="color:black">:</span>
 
  
−
<div style="border:0px solid black;display:inline-table;margin-left: 10px;"> [[Image: 6_Exakta_trig_varden.jpg]] </div>
 
  
  
−
<big><b><span style="color:#931136">Enhetscirkeln</span></b></big>
 
  
−
''Cirkel'' <math> \, = \, </math> Mängden av alla punkter som har samma avstånd (radien <math> \, r \, </math>) från en punkt (medelpunkten <math> \, M \, </math>).
 
  
−
Cirkelns ekvation:
 
  
−
<div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 7_Cirkelns_ekvation_70.jpg]] </div>
 
  
  
−
''Enhetscirkeln'' är cirkeln med radien <math> \, r \, = \, 1 \, </math> och medelpunkten <math> \, M \, = \, O \, </math> (origo).
+
 
 +
 
 +
 
 +
 
 +
</td>
 +
</tr>
 +
</table>
 +
 
 +
 
 +
== <b><span style="color:#931136">1.2 Trigonometri i godtyckliga trianglar</span></b> ==
 +
{| border="0" cellspacing="0" cellpadding="0" height="30" width="150%"
 +
| style="border-bottom:1px solid #797979" width="5px" | &nbsp;
 +
{{Not selected tab|[[Repetition_Trigonometri#1.1_Trigonometri_i_r.C3.A4tvinkliga_trianglar|<<&nbsp;&nbsp;Förra avsnitt: Genomgång rätvinkliga]]}}
 +
{{Not selected tab|[[Formelsamling Matte 4 Trigonometri|Formelsamling Trigonometri]]}}
 +
{{Not selected tab|[[1.3 Trigonometriska identiteter|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
 +
| style="border-bottom:1px solid #797979"  width="150%"| &nbsp;
 +
|}
 +
 
 +
 
 +
=== <span style="color:#931136">Enhetscirkeln</span> ===
 +
är cirkeln med radien <math> \, r \, = \, 1 \, </math> och medelpunkten <math> \, M \, = \, O \, </math> (origo).
  
 
Om en punkt <math> \, P\,(x, y) \, </math> snurrar på enhetscirkeln och <math> \, v \, </math> är vinkeln mellan <math> \, x</math>-axeln och <math> \, \overline{OP} </math>, så gäller<span style="color:black">:</span>
 
Om en punkt <math> \, P\,(x, y) \, </math> snurrar på enhetscirkeln och <math> \, v \, </math> är vinkeln mellan <math> \, x</math>-axeln och <math> \, \overline{OP} </math>, så gäller<span style="color:black">:</span>
Rad 106: Rad 102:
 
</tr>
 
</tr>
 
</table>
 
</table>
−
I cirklar med radien <math> \, r \, > \, 1 \, </math> förblir vinkeln <math> \, v \, </math> den samma och därmed <math> \, \cos v = \displaystyle \frac{r \cdot \; x}{r} = x \, </math> och <math> \, \sin v = \displaystyle \frac{r \cdot \; y}{r} = y </math>, precis som ovan.
+
I cirklar med radien <math> \, r \, > \, 1 \, </math> förblir vinkeln <math> \, v \, </math> den samma och därmed <math> \, \cos v = (r \cdot x) / r = x \, </math> och <math> \, \sin v = (r \cdot y) / r = y </math>, precis som ovan.
  
−
Detta används för att definiera de trigonometriska funktionerna i godtyckliga trianglar, dvs för vinklar <math> \, v \, \geq \, 90^\circ \, </math>.
+
Dvs formlerna för <math> \, x = \cos v \, </math> och <math> \, y = \sin v \, </math> stämmer fortfarande, även om <math> \, r \, > \, 1 \, </math>.
  
 +
De här formlerna används för att definiera de trigonometriska funktionerna i godtyckliga trianglar, dvs för vinklar <math> \, v \, \geq \, 90^\circ \, </math>.
  
−
== <b><span style="color:#931136">5.3 Godtyckliga trianglar <math> \qquad\qquad\;\; </math> <small><small>Övningar: &nbsp; Boken, sid 215 </small></small></span></b> ==
 
 
<br>
 
<br>
 
<big><b><span style="color:#931136">Sinus och Cosinus för vinklar i intervallet<span style="color:#931136">:</span> <math> \quad 90^\circ \, \leq \, v \, \leq \, 180^\circ </math> </span></b></big>
 
<big><b><span style="color:#931136">Sinus och Cosinus för vinklar i intervallet<span style="color:#931136">:</span> <math> \quad 90^\circ \, \leq \, v \, \leq \, 180^\circ </math> </span></b></big>
  
 
Exempel<span style="color:black">:</span>
 
Exempel<span style="color:black">:</span>
−
:::<math> \sin 150^\circ \, = \, \sin (180^\circ - 30^\circ) \, = \, \sin 30^\circ \, = \, \frac{1}{2} </math>
+
:::<math> \sin 150^\circ \, = \, \sin (180^\circ - 30^\circ) \, = \, \sin 30^\circ \, = \, 1 / 2 </math>
−
:::<math> \cos 120^\circ \, = \, \cos (180^\circ - 60^\circ) \, = \, -\cos 60^\circ \, = \, -\frac{1}{2} </math>
+
:::<math> \cos 120^\circ \, = \, \cos (180^\circ - 60^\circ) \, = \, -\cos 60^\circ \, = \, -(1 / 2) </math>
 
Förklaring med enhetscirkeln:
 
Förklaring med enhetscirkeln:
  
Rad 168: Rad 164:
  
  
−
<big><b><span style="color:#931136">Sinus, Cosinus och Tangens för alla vinklar</span></b></big>
+
=== <span style="color:#931136">Sinus, Cosinus och Tangens för alla vinklar</span> ===
 
<table>
 
<table>
 
<tr>
 
<tr>
Rad 218: Rad 214:
 
</tr>
 
</tr>
 
</table>
 
</table>
 +
<big><big><b><span style="color:#931136">Slutsatser</span></b></big></big>
  
 
<div class="border-divblue">En <b><span style="color:red">sinus</span></b>ekvation har i intervallet <math> \, 0^\circ \leq v \leq 180^\circ \, </math> alltid <b><span style="color:red">två</span></b> lösningar.<br><br>
 
<div class="border-divblue">En <b><span style="color:red">sinus</span></b>ekvation har i intervallet <math> \, 0^\circ \leq v \leq 180^\circ \, </math> alltid <b><span style="color:red">två</span></b> lösningar.<br><br>
 
En <b><span style="color:red">cosinus</span></b>ekvation har i intervallet <math> \, 0^\circ \leq v \leq 180^\circ \, </math> <b><span style="color:red">endast en</span></b> lösning.</div>
 
En <b><span style="color:red">cosinus</span></b>ekvation har i intervallet <math> \, 0^\circ \leq v \leq 180^\circ \, </math> <b><span style="color:red">endast en</span></b> lösning.</div>
 +
</big>
  
  
−
== <b><span style="color:#931136">5.4 Triangelsatserna <math> \qquad\qquad\qquad\;\; </math> <small><small>Övningar: &nbsp; Boken, sid 218 </small></small></span></b> ==
 
  
  
−
Det finns tre triangelsatser: <b><span style="color:#931136">Areasatsen</span></b>, <b><span style="color:#931136">Sinussatsen</span></b> och <b><span style="color:#931136">Cosinussatsen</span></b>.
 
  
−
Triangelsatsernas formulering baseras på de standardbeteckningar för trianglar som införs här:
 
  
−
<big><b><span style="color:#931136">Areasatsen</span></b></big>
 
  
−
<u>Givet:</u> <math> \quad </math>  Två sidor och den mellanliggande vinkeln i en triangel.
 
  
−
<u>Sökt:</u> <math> \quad\, </math> Triangelns area.
 
  
−
<table>
 
−
<tr>
 
−
  <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 11 Areasatsen_400_0b.jpg]]</div>
 
  
  
  
−
</td>
 
−
<td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;</td>
 
−
  <td>
 
−
<div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 11 Areasatsen_400a.jpg]]</div>
 
−
 
−
&nbsp; Areasatsen i vanliga ord (utan beteckningar):
 
−
 
−
<div class="border-divblue">En triangels area är produkten av <b><span style="color:red">två sidor</span></b>
 
−
 
−
och den <b><span style="color:red">mellanliggande vinkelns</span></b> sinus,
 
−
 
−
delad med <math> \, 2 \, </math> (<b><span style="color:red">SVS</span></b>-struktur).</div>
 
−
</td>
 
−
</tr>
 
−
</table>
 
−
<big><b><span style="color:#931136">Det omvända problemet:</span></b></big>
 
−
 
−
<u>Givet:</u> <math> \quad </math> Arean och två sidor av en triangel.
 
−
 
−
<u>Sökt:</u> <math> \quad\, </math> Den mellanliggande vinkeln <math> \, v \, </math>.
 
−
<table>
 
−
<tr>
 
−
  <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 11 Areasatsen_400_0c.jpg]]</div>
 
−
 
−
</td>
 
−
<td>&nbsp;&nbsp;&nbsp;&nbsp;</td>
 
−
  <td>
 
−
 
−
 
−
 
−
 
−
 
−
 
−
<div class="ovnE">
 
−
{{#NAVCONTENT:Varför två lösningar?|Varför två lösningar}}
 
−
</div>
 
−
</td>
 
−
</tr>
 
−
</table>
 
−
Det geometriska problemet har två lösningar. Areasatsen ger båda:
 
−
 
−
Areasatsen leder till en sinusekvation som pga sina två lösningar resulterar i två vinklar och därmed två trianglar.
 
−
 
−
 
−
== <b><span style="color:#931136">5.5 Sinussatsen <math> \qquad\qquad\qquad\;\; </math> <small><small>Övningar: &nbsp; Boken, sid 220 / 224-225 </small></small></span></b> ==
 
−
 
−
<u>Givet:</u> <math> \quad </math>  Två sidor och en vinkel eller två vinklar och en sida i en triangel.
 
−
 
−
<u>Sökt:</u> <math> \quad\, </math> Triangelns tredje sida eller två andra sidor.
 
−
 
−
<table>
 
−
<tr>
 
−
  <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 12 Sinussatsen_400.jpg]] </div>
 
−
 
−
</td>
 
−
<td>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;</td>
 
−
  <td>
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
Sinussatsen i vanliga ord (utan beteckningar):
 
−
 
−
<div class="border-divblue">I en triangel är kvoten mellan
 
−
 
−
vinklarnas sinus och deras
 
−
 
−
motstående sidor lika stor.</div>
 
−
 
−
</td>
 
−
</tr>
 
−
</table>
 
−
 
−
==== <b><span style="color:#931136">Exempel på sinussatsen (två lösningar)</span></b> ====
 
−
 
−
<u>Givet:</u> <math> \quad </math>  Två sidor och den vinkel som inte ligger mellan dem (icke-SVS-struktur).
 
−
 
−
<u>Sökt:</u> <math> \quad\, </math> Triangelns tredje sida.
 
−
 
−
<table>
 
−
<tr>
 
−
  <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 12 Sinussatsens_2_fall_400.jpg]] </div>
 
−
</td>
 
−
<td>&nbsp;&nbsp;</td>
 
−
  <td>
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
<div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 12 Tva trianglar.jpg]] </div>
 
−
</td>
 
−
<td>
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
<div class="ovnE">
 
−
{{#NAVCONTENT:Varför två lösningar?|Varför två lösningar}}
 
−
</div>
 
−
</td>
 
−
</tr>
 
−
</table>
 
−
Att det finns två lösningar (två trianglar) beror på att problemet inte har [[Kapitel_5_Trigonometri#5.4_Triangelsatserna_.5C.28_.5Cqquad.5Cqquad.5Cqquad.5C.3B.5C.3B_.5C.29_.C3.96vningar:_.C2.A0_Boken.2C_sid_218|<b><span style="color:blue">SVS</span></b>]]-struktur, dvs:
 
−
 
−
Triangelns två sidor <math> \, b = 27 \, </math> och <math> \, c = 35 \, </math> är givna, men inte den mellanliggande vinkeln, utan den som ligger mittemot <math> \, b </math>.
 
−
 
−
 
−
== <b><span style="color:#931136">5.6 Cosinussatsen <math> \qquad\qquad\qquad\;\; </math> <small><small>Övningar: &nbsp; Boken, sid 229-230 </small></small></span></b> ==
 
−
 
−
<u>Givet:</u> <math> \quad </math>  Två sidor och en vinkel i en triangel.
 
−
 
−
<u>Sökt:</u> <math> \quad\, </math> Triangelns tredje sida.
 
−
 
−
<table>
 
−
<tr>
 
−
  <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 13 Cosinussatsen_400.jpg]] </div>
 
−
 
−
</td>
 
−
<td>&nbsp;&nbsp;&nbsp;&nbsp;</td>
 
−
  <td>
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
<div class="border-divblue">Cosinussatsen utvidgar Pythagoras med
 
−
 
−
en <math> \cos</math>-term som involverar högerledets
 
−
 
−
två sidor och den mellanliggande vinkeln.</div>
 
−
 
−
</td>
 
−
</tr>
 
−
</table>
 
−
 
−
Pythagoras är ett specialfall av cosinussatsen för fallet<span style="color:black">:</span> <math> \; A , B , {\rm eller\;} C \, = \, 90^\circ \; \Rightarrow \; \cos 90^\circ \, = \, 0 </math>. Då försvinner <math> \cos</math>-termen i cosinussatsen.
 
−
 
−
När två sidor och den mellanliggande vinkeln i en triangel är givna ([[Kapitel_5_Trigonometri#5.4_Triangelsatserna_.5C.28_.5Cqquad.5Cqquad.5Cqquad.5C.3B.5C.3B_.5C.29_.C3.96vningar:_.C2.A0_Boken.2C_sid_218|<b><span style="color:blue">SVS</span></b>]]-struktur), ger cosinussatsen den tredje sidan som roten ur högerledet: <b><span style="color:red">endast en lösning</span></b>.
 
−
 
−
När två sidor är givna samt en vinkel som inte ligger mellan dem (icke-SVS-struktur) ger cosinussatsen en andragradsekvation som i regel har <b><span style="color:red">två lösningar</span></b>, se exemplet nedan.
 
−
 
−
<big><b><span style="color:#931136">Samma exempel som [[Kapitel_5_Trigonometri#Exempel_p.C3.A5_sinussatsen_.28tv.C3.A5_l.C3.B6sningar.29|<span style="color:blue">ovan</span>]], nu med cosinussatsen</span></b></big>
 
−
 
−
<div style="border:0px solid black;display:inline-table;margin-left: 10px;"> [[Image: 13 Ex Cosinussatsen_1_400.jpg]] </div><br>
 
−
<table>
 
−
<tr>
 
−
  <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 13 Ex Cosinussatsen_2_400.jpg]] </div>
 
−
 
−
</td>
 
−
<td>&nbsp;&nbsp;&nbsp;&nbsp;</td>
 
−
  <td>
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
<div class="ovnE">
 
−
{{#NAVCONTENT:Varför två lösningar?|Varför två lösningar}}
 
−
</div>
 
−
 
−
</td>
 
−
</tr>
 
−
</table>
 
−
 
−
Cosinussatsen ger samma två lösningar som sinussatsen, se [[Kapitel_5_Trigonometri#Exempel_p.C3.A5_sinussatsen_.28tv.C3.A5_l.C3.B6sningar.29|<b><span style="color:blue">ovan</span></b>]].
 
−
 
−
 
−
== <b><span style="color:#931136">5.7 Användning av trigonometri <math> \qquad\qquad\;\; </math> <small><small>Övningar: &nbsp; Boken, sid 232-233 </small></small></span></b> ==
 
−
<br>
 
−
<table>
 
−
<tr>
 
−
  <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;">[[Image: 14 Spiraltrappa_750.jpg]]</div>
 
−
 
−
</td>
 
−
  <td>
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
 
−
<div class="ovnE">
 
−
{{#NAVCONTENT:Svar|5.7 Svar fel i 5.7}}
 
−
</div>
 
−
</td>
 
−
</tr>
 
−
</table>
 
−
 
−
 
−
<table>
 
−
<tr>
 
−
  <td><div style="border:1px solid black;display:inline-table;margin-left: 10px;">[[Image: 233 Uppg 4269 Femhorn 4270 Klippa-1_400.jpg]] </div>
 
−
 
−
 
−
 
−
 
−
</td>
 
−
  <td><div style="border:1px solid black;display:inline-table;margin-left: 20px;">[[Image: 233 Uppg 4269 Femhorn 4270 Klippa-2_400.jpg]] </div></td>
 
−
</tr>
 
−
</table>
 
−
 
−
 
−
<div style="border:1px solid black;display:inline-table;margin-left: 10px;">
 
−
<table>
 
−
<tr>
 
−
  <td>[[Image: 14_2_Balong_Uppg_450.jpg]]
 
−
 
−
::<math> \underline{\rm Lösning:} \quad {\rm Vi\;ritar\;figuren\;till\;höger\;(modellering).} </math>
 
−
 
−
::<math>{\rm Sidovinkeln} \quad u \, = \, 180^\circ - 72,5^\circ \, = \, 107,5^\circ </math>
 
−
 
−
::<math>{\rm Vinkelsumman\;i\;triangeln\;} ABC {\rm \;ger} </math>
 
−
 
−
::<math> v \, = \, 180^\circ - 56,4^\circ - 107,5^\circ\, = \, 16,1^\circ </math></td>
 
−
  <td>[[Image: 14_2_Balong_Bild_300.jpg]]</td>
 
−
</tr>
 
−
</table>
 
−
:[[Image: 14_2_Balong_Losning_450.jpg]]</div>
 
−
 
−
 
−
</big>
 
  
  
Rad 570: Rad 237:
  
  
−
[[Matte:Copyrights|Copyright]] © 2011-2019 Math Online Sweden AB. All Rights Reserved.
+
[[Matte:Copyrights|Copyright]] © 2021 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved.

Nuvarande version från 26 april 2025 kl. 20.08

       Innehållsförteckning          1.1 Rätvinkliga trianglar          Övningar          1.2 Godtyckliga trianglar          1.3 Trigon. identiteter  >>      


Trigon = Triangel på latin. \( \qquad\qquad\qquad\qquad\quad \) Trigonometri = Att mäta trianglar.

1.1 Trigonometri i rätvinkliga trianglar

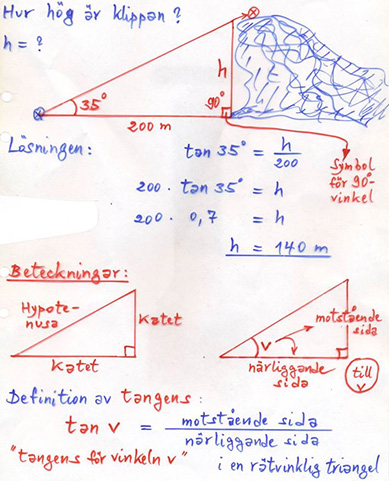
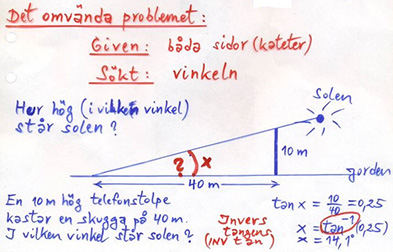
Tangens för \( \, v \, < \, 90^\circ \)

1 Tangens 55.jpg

Se även längre ned.


Sinus och Cosinus för \( \, v \, < \, 90^\circ \)

5 SinusCosinus 55.jpg
2 Tangensproblemet 55.jpg


  
3 OmvantProblem 55.jpg















1.2 Trigonometri i godtyckliga trianglar

       <<  Förra avsnitt: Genomgång rätvinkliga          Formelsamling Trigonometri          Nästa avsnitt  >>      


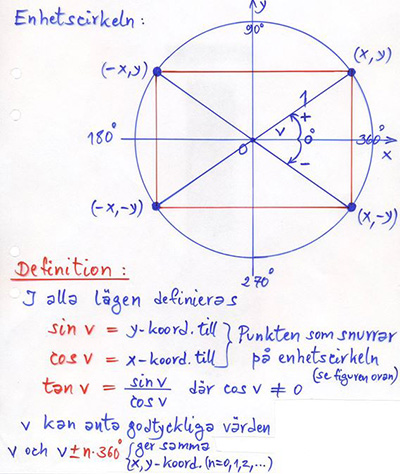
Enhetscirkeln

är cirkeln med radien \( \, r \, = \, 1 \, \) och medelpunkten \( \, M \, = \, O \, \) (origo).

Om en punkt \( \, P\,(x, y) \, \) snurrar på enhetscirkeln och \( \, v \, \) är vinkeln mellan \( \, x\)-axeln och \( \, \overline{OP} \), så gäller:

7 Enhetscirkeln.jpg
\( \qquad\qquad\quad \)
\(\begin{array}{rcl} x & = & \cos v \\ y & = & \sin v \end{array}\)

I cirklar med radien \( \, r \, > \, 1 \, \) förblir vinkeln \( \, v \, \) den samma och därmed \( \, \cos v = (r \cdot x) / r = x \, \) och \( \, \sin v = (r \cdot y) / r = y \), precis som ovan.

Dvs formlerna för \( \, x = \cos v \, \) och \( \, y = \sin v \, \) stämmer fortfarande, även om \( \, r \, > \, 1 \, \).

De här formlerna används för att definiera de trigonometriska funktionerna i godtyckliga trianglar, dvs för vinklar \( \, v \, \geq \, 90^\circ \, \).


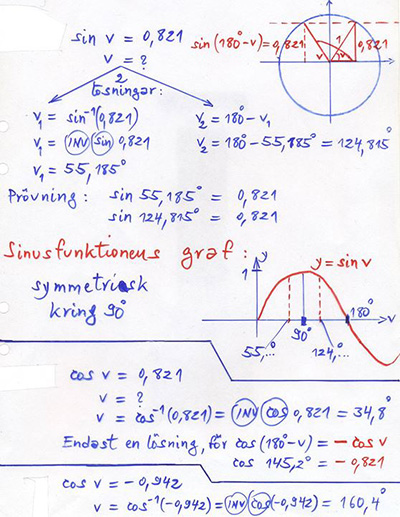
Sinus och Cosinus för vinklar i intervallet: \( \quad 90^\circ \, \leq \, v \, \leq \, 180^\circ \)

Exempel:

\[ \sin 150^\circ \, = \, \sin (180^\circ - 30^\circ) \, = \, \sin 30^\circ \, = \, 1 / 2 \]
\[ \cos 120^\circ \, = \, \cos (180^\circ - 60^\circ) \, = \, -\cos 60^\circ \, = \, -(1 / 2) \]

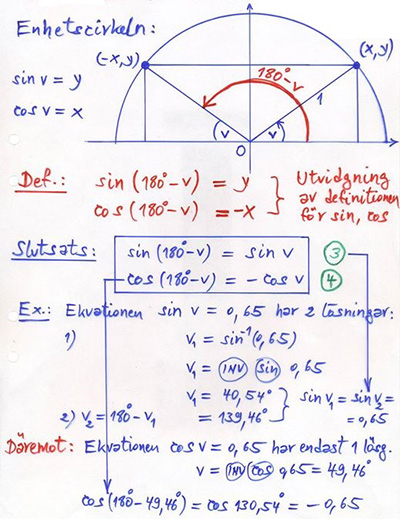
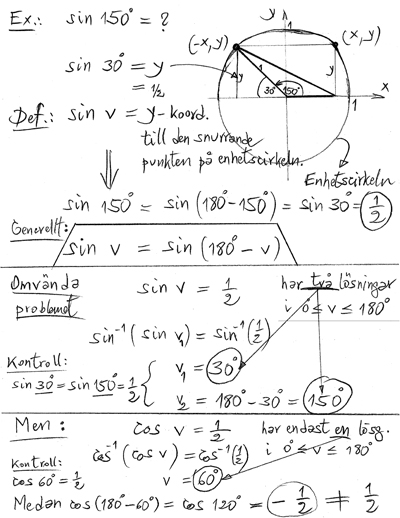
Förklaring med enhetscirkeln:

Punkten till vinkeln \( \, v \, \) har samma \( \, y\)-koordinat (\(=\sin v\)) som punkten till vinkeln \( \, 180-v \).

Punkten till vinkeln \( \, v \, \) har samma \( \, x\)-koordinat (\(=\cos v\)) som punkten till vinkeln \( \, 180-v \, \) med omvänt tecken.

8 Godtyckliga trianglar 400.jpg
   Ekvationer  

        med

   Sin & Cos:















9 Ex Godtyckliga vinklar 400.jpg


Sinus, Cosinus och Tangens för alla vinklar

10 Alla vinklar 400.jpg



  En gång till  

   Sin & Cos

  för \( v \geq 90^\circ \)

   i trianglar:














10a En gang till Sin Cos 400.jpg


Slutsatser

En sinusekvation har i intervallet \( \, 0^\circ \leq v \leq 180^\circ \, \) alltid två lösningar.

En cosinusekvation har i intervallet \( \, 0^\circ \leq v \leq 180^\circ \, \) endast en lösning.










Copyright © 2021 TechPages AB. All Rights Reserved.

Hämtad från "https://matte4.mathonline.se/index.php?title=Repetition_Trigonometri&oldid=11499"