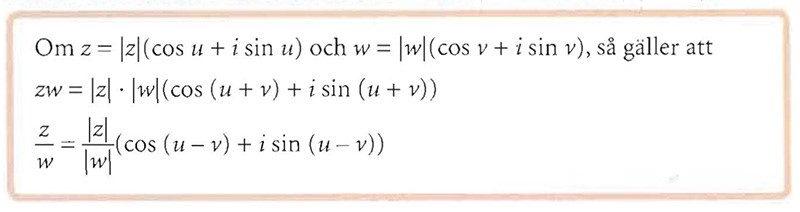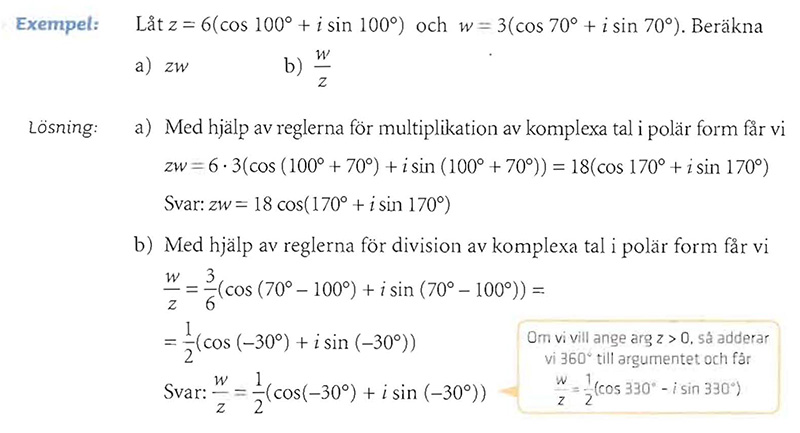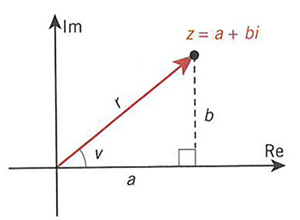
Repetition: Komplexa tal på polär form

För att hitta z: Gå från Origo r steg i riktning v

\( \quad \)

\( z \, = \, a + b \, i \, = \, r \, (cos\,v + i \, sin\,v) \)

\( r \; = \; | z | \; = \; \sqrt{a^2 + b^2} \)

\( \tan v \, = \, b/a \; \implies \; v \, = \, \tan^{-1} (b/a) \)

Ex.: \( \quad\; z \, = \, 3 + 4 \, i \; \implies \; r \; = \; | z | \; = \; \sqrt{3^2 + 4^2} \; = \; 5 \) \( \qquad\qquad\qquad\qquad\;\, \implies \; v \; = \; \tan^{-1} (4/3) \; = \; 53,13^\circ \) \( \qquad\quad z \, = \, 5 \, (cos\,53,13^\circ + i \, sin\,53,13^\circ) \) Omvänt: \( \quad\; a \, = \, \)

Multiplikation och division av komplexa tal i polär form

Regler

Multiplicera absolutbeloppen och addera argumenten.

Dividera absolutbeloppen och subtrahera argumenten.

I formler:

Multiplikation

Multiplikation & division

4.9 Multiplikation och division i polär form