Genomgång

Övningar

Facit

Innehållsförteckning

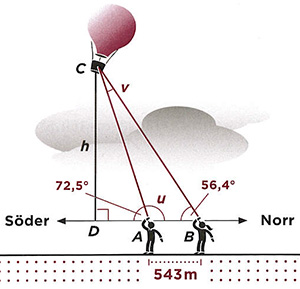
Användning av trigonometri

Oljetank med spiraltrappa

Fil:14 Spiraltrappa 800.jpg

Lösning

$\underline{\rm Lösning:} \quad {\rm Vi\;ritar\;figuren\;till\;höger\;(modellering).}$

${\rm Sidovinkeln} \quad u \, = \, 180^\circ - 72,5^\circ \, = \, 107,5^\circ$

${\rm Vinkelsumman\;i\;triangeln\;} ABC {\rm \;ger}$

$v \, = \, 180^\circ - 56,4^\circ - 107,5^\circ\, = \, 16,1^\circ$

Triangelsatserna

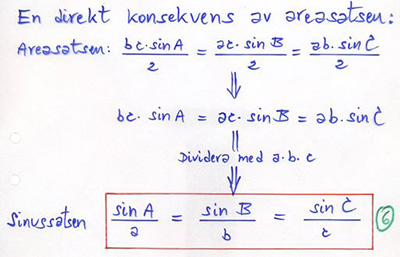
Det finns tre triangelsatser: Areasatsen, Sinussatsen och Cosinussatsen.

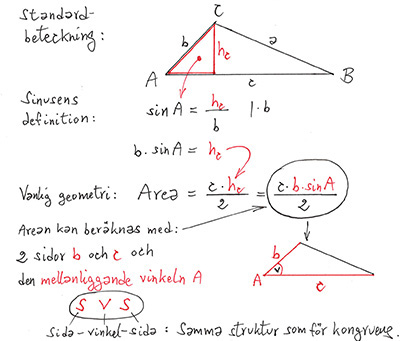
Triangelsatsernas formulering baseras på de standardbeteckningar för trianglar som införs här:

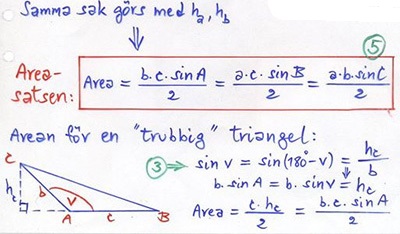
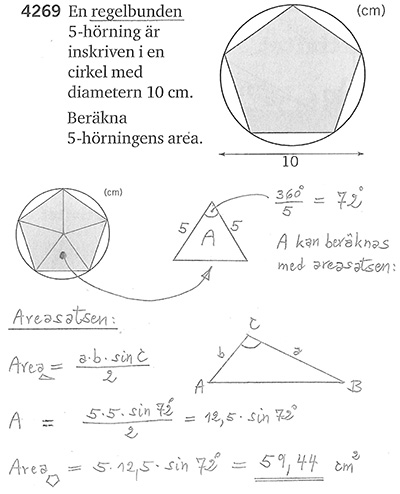
Areasatsen

Givet: $\quad$ Två sidor och den mellanliggande vinkeln i en triangel.

Sökt: $\quad\,$ Triangelns area.

Areasatsen i vanliga ord (utan beteckningar):

En triangels area är produkten av två sidor

och den mellanliggande vinkelns sinus,

delad med

$\, 2 \,$ (SVS-struktur).

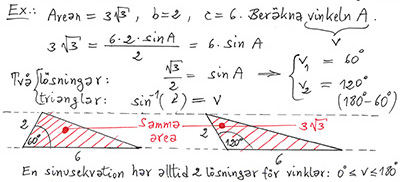
Det omvända problemet:

Givet: $\quad$ Arean och två sidor av en triangel.

Sökt: $\quad\,$ Den mellanliggande vinkeln $\, v \,$ .

Varför två lösningar?

Det geometriska problemet har två lösningar. Areasatsen ger båda:

Areasatsen leder till en sinusekvation som pga sina två lösningar resulterar i två vinklar och därmed två trianglar.

Sinussatsen

Givet: $\quad$ Två sidor och en vinkel eller två vinklar och en sida i en triangel.

Sökt: $\quad\,$ Triangelns tredje sida eller två andra sidor.

Sinussatsen i vanliga ord (utan beteckningar):

I en triangel är kvoten mellan

vinklarnas sinus och deras

motstående sidor lika stor.

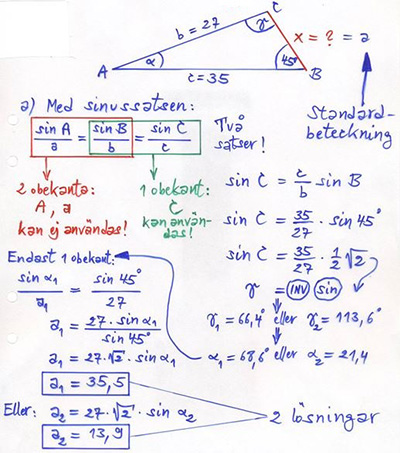
Exempel på sinussatsen (två lösningar)

Givet: $\quad$ Två sidor och den vinkel som inte ligger mellan dem (icke-SVS-struktur).

Sökt: $\quad\,$ Triangelns tredje sida.

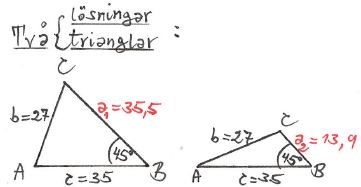
Varför två lösningar?

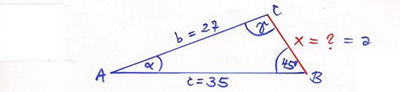
Att det finns två lösningar (två trianglar) beror på att problemet inte har SVS-struktur, dvs:

Triangelns två sidor $\, b = 27 \,$ och $\, c = 35 \,$ är givna, men inte den mellanliggande vinkeln, utan den som ligger mittemot $\, b$ .

Cosinussatsen

Givet: $\quad$ Två sidor och en vinkel i en triangel.

Sökt: $\quad\,$ Triangelns tredje sida.

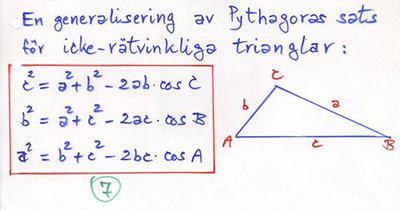
Cosinussatsen utvidgar Pythagoras med

en $\cos$ -term som involverar högerledets

två sidor och den mellanliggande vinkeln.

Pythagoras är ett specialfall av cosinussatsen för fallet $\; A , B , {\rm eller\;} C \, = \, 90^\circ \; \Rightarrow \; \cos 90^\circ \, = \, 0$ . Då försvinner $\cos$ -termen i cosinussatsen.

När två sidor och den mellanliggande vinkeln i en triangel är givna (SVS-struktur), ger cosinussatsen den tredje sidan som roten ur högerledet: endast en lösning.

När två sidor är givna samt en vinkel som inte ligger mellan dem (icke-SVS-struktur) ger cosinussatsen en andragradsekvation som i regel har två lösningar, se exemplet nedan.

Samma exempel som ovan, nu med cosinussatsen