4.17 Polynomekvationer av högre grad
IND_VAL: v14 I, tis kl 11.15-12.20, sal 10. Övningar 4444-4457.
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
Algebrans fundamentalsats
Ett polynom av grad \( n\, \) har exakt \( n\, \) komplexa nollställen \( \; x_1, \, x_2, \,\ldots\, , x_n \; \) och kan faktoriseras så här:
\( a_n \, x^n \,+\, a_{n-1} \, x^{n-1} + \quad \ldots \quad + a_1 \, x \,+\, a_0 \quad = \quad {\color{Red} {a_n \cdot\, (x-x_1) \,\cdot\, (x-x_2) \,\cdot\quad\ldots\quad \cdot\, (x-x_n)}} \)
Se bevis, historia & annat gott.
Anmärkningar:
- Fundamentalsatsens egentliga utsaga är: Ett polynom av grad \( n\, \) har exakt \( n\, \) komplexa nollställen. Den ska tolkas så här:
- Antalet \( n\, \) borde räknas med multiplicitet, dvs dubbla rötter är räknade två gånger, tredubbla tre gånger osv.
- Den fullständiga faktoriseringen i linjära faktorer \( (x-x_i)\, \) där \( x_i\, \) = polynomets nollställen, är endast möjlig i mängden av komplexa tal.
- Räknar man endast med reella tal kommer vissa polynom att faktoriseras till linjära och kvadratiska faktorer, där de kvadratiska faktorerna har komplexa rötter.
Exempel 1
Faktorisera följande polynom fullständigt:
\( P(x) = x^4 - 29\;x^2 + 100 \)
I övning 6 till repetitionsavsnittet Ekvationer hade vi löst 4:e gradsekvationen
\( x^4 - 29\;x^2 = -100 \)
och fått lösningarna
\( x_1 = 5, \qquad x_2 = -5, \qquad x_3 = 2 \quad {\rm och} \quad x_4 = -2 \)
Vi kan skriva ekvationen som en polynomekvation
\( P(x) = x^4 - 29\;x^2 + 100 = 0 \)
Pga kännedomen om ekvationens lösningar som är identiska med polynomets nollställen, kan vi enligt algebrans fundamentalsats faktorisera 4:e gradspolynomet \( P(x)\, \) så här\[ P(x) = x^4 - 29\;x^2 + 100 = (x-5) \cdot (x+5) \cdot (x-2) \cdot (x+2) \]
Exempel 2
Faktorisera polynomet \( P(x)\, \) fullständigt när följande delfaktorisering redan existerar:
- \[ P(x) = x^5 - 5\,x^4 + 17\,x^3 - 13\,x^2 = x\cdot x\cdot (x-1)\cdot (x^2 - 4\,x + 13) \]
Delfaktoriseringen visar en dubbelrot \( x = 0\, \) och en enkel rot \( x = 1\, \). Man kan få fram den med de metoder vi lärt oss i detta avsnitt: Den dubbla roten \( x = 0\, \) får man genom att bryta ut \( x^2 \). Den enkla roten \( x = 1\, \) kan man få via grafen samt en prövning. Den sista faktorn kan beräknas med hjälp av jämförelse av koefficienter. Denna delfaktorisering stannar inom ramen av de reella talen.
Enligt algebrans fundamentalsats måste 5:e gradspolynomet \( P(x)\, \) ha två rötter till som ger upphov till den kvadratiska faktorn \( x^2 - 4\,x + 13 \) som står sist.
Vill man gå vidare och få fram den fullständiga faktoriseringen i linjära faktorer måste även den kvadratiska faktorn faktoriseras. Detta innebär att vi måste beräkna dess rötter som visar sig vara komplexa:
- \[\begin{array}{rcl} x^2 - 4\,x + 13 & = & 0 \\ x_{1,2} & = & 2 \pm \sqrt{4 - 13} \\ x_{1,2} & = & 2 \pm \sqrt{-9} \\ x_{1,2} & = & 2 \pm \sqrt{9 \cdot (-1)} \\ x_{1,2} & = & 2 \pm \sqrt{9}\cdot \sqrt{-1} \\ x_1 & = & 2 + 3\,i \\ x_2 & = & 2 - 3\,i \\ \end{array}\]
Vi får alltså följande faktorisering av den kvadratiska faktorn:
- \[ x^2 - 4\,x + 13 = (x - (2+3\,i)) \cdot (x - (2-3\,i)) = (x - 2-3\,i) \cdot (x - 2+3\,i)\]
Därmed blir den fullständiga faktoriseringen av polynomet \( P(x)\, \) i linjära faktorer\[ P(x) = x^5 - 5\,x^4 + 17\,x^3 - 13\,x^2 = x\cdot x\cdot (x-1)\cdot (x - 2-3\,i) \cdot (x - 2+3\,i) \]
Dvs \( P(x)\, \) har förutom dubbelroten \( x = 0\, \) och den enkla roten \( x = 1\, \) även de två komplexa rötterna \( x = 2 + 3\,i \) och \( x = 2 - 3\,i \). Sammanlagt har 5:e gradspolynomet \( P(x)\, \) exakt 5 rötter, om man räknar rötterna med multiplicitet, dvs den dubbla rotter dubbelt och beräknar även de komplexa rötterna - i enlighet med algebrans fundamentalsats.
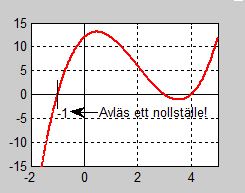
Exempel
|
Faktorisera polynomet \( \qquad P(x) \; = \; x^3 - 6\,x^2 + 5\,x + 12 \)
Grafen visar att polynomet har tre nollställen av vilka ett kan avläsas till \( \, x_1 = -1 \). För att avgöra om detta nollställe är exakt gör vi en kon- troll genom att sätta in \( \, x_1 = -1 \, \) i polynomet: | \( \quad \) |  |
\( P(-1) = (-1)^3 - 6\,\cdot\,(-1)^2 + 5\,\cdot\,(-1) + 12 = -1 - 6\,\cdot\,1 - 5 + 12 = -12 +12 = 0 \)
Kontrollen visar att \( x_1 = -1\, \) är ett exakt nollställe till \( P(x) \). Slutsats: Faktorn \( \, (x + 1) \, \) kan brytas ut:
- \[ P(x) \; = \; x^3 - 6\,x^2 + 5\,x + 12 \; = \; Q(x) \cdot (x+1) \; = \; 0 \]
där \( \, Q(x) \, \) är ett 2:a gradspolynom som vi inte känner till än, se algebrans fundamentalsats.
\( P(x)\, \):s två andra nollställen måste vara det 2:a gradspolynomet \( \, Q(x)\, \):s nollställen.
Vi bestämmer \( \, Q(x)\, \) genom att sätta den till den allmänna formen för 2:a gradspolynom:
- \[ Q(x) = a\,x^2 + b\,x + c \]
där \( \, a, b, c \, \) är koefficienter som vi måste bestämma. Sätter vi in denna form i ansasten ovan får vi:
- \[ x^3 - 6\,x^2 + 5\,x + 12 = (a\,x^2 + b\,x + c) \cdot (x+1) \]
Vi bestämmer \( \, a, b, c \, \) genom lösa upp parentesen och jämföra koefficienterna:
- \[ x^3 - 6\,x^2 + 5\,x + 12 = a\,x^3 + b\,x^2 + c\,x + a\,x^2 + b\,x + c = a\,x^3 + (b+a)\,x^2 + (c+b)\,x + c \]
Jämförelse av koefficienterna på höger- och vänsterled ger:
- \[ \begin{align} a & = 1 \\ b + a & = -6 \\ c + b & = 5 \\ c & = 12 \end{align}\]
Genom insättning av \( \, a = 1 \, \) i den andra och \( \, c = 12 \, \) i den tredje ekvationen får vi i båda fall \( \, b = -7 \, \).
Därmed har vi bestämt polynomet \( \, Q(x) \, \):
- \[ Q(x) = x^2 - 7\,x + 12 \]
I Faktorisering av 2:a gradspolynom hade vi faktoriserat \( \, Q(x) \, \) så här:
- \[ x^2 - 7\,x + 12 = (x-3) \cdot (x-4) \]
där \( \, x_2 = 3 \, \) och \( \, x_3 = 4 \, \) är \( \, Q(x)\, \):s nollställen.
Inför vi nu detta resultat i vår ansats i början får vi den fullständiga faktoriseringen för \( \, P(x) \):
\( P(x) = x^3 - 6\,x^2 + 5\,x + 12 = Q(x) \cdot (x+1) = (x^2 - 7\,x + 12) \cdot (x+1) = \underline{(x-3)\,\cdot\,(x-4)\,\cdot\,(x+1)} \)
Den ovan beskrivna metoden kan i princip även användas för faktorisering av polynom av högre grad än 3.
Till grund för alla dessa faktoriseringar ligger algebrans fundamentalsats som behandlades ovan.
Copyright © 2022 TechPages AB. All Rights Reserved.
