4.15 Polynomdivision

<<  Förra avsnitt

Genomgång

Övningar

Facit

Nästa avsnitt  >>

Manuell division av heltal med rest $\; \neq 0$

Manuell division av heltal utan rest

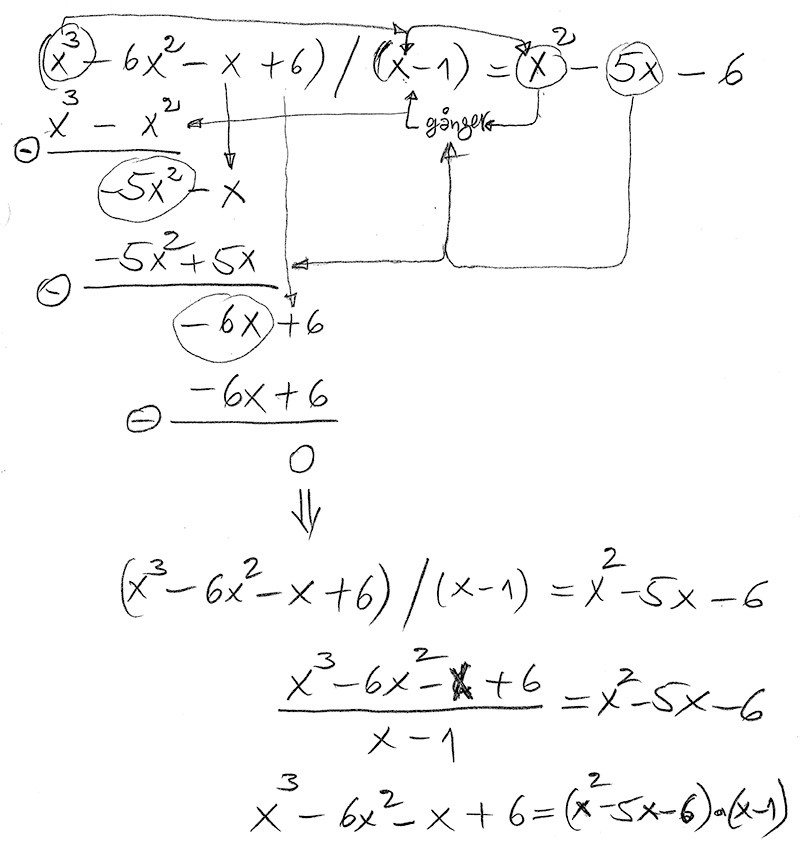
Manuell division av polynom utan rest

Dividera $\; x^3 - 6 x^2 - x + 6 \;$ med $\; x - 1$

Jämförelse av koefficienter, en alternativ metod för polynomdivision utan rest

Uppgift: $\qquad$ Utför polynomdivisionen $\quad (x^3 + 4\,x^2 + x - 26) \; / \; (x-2)$

En annan formulering av uppgiften är:

Hitta ett 2:a gradspolynom $\, Q(x)\,$ så att $\, Q(x)\cdot (x-2) = (x^3 + 4\,x^2 + x - 26)$

Lösning:

Vi inför beteckningen: $\quad\;\;\, P(x) = x^3 + 4\,x^2 + x - 26$.

$Q(x)\,$ kan skrivas så här (Ansats): $\qquad Q(x) = a\,x^2 + b\,x + c$

Vi bestämmer koefficienterna $a\, , \, b\,$ och $c\,$ så att $\; Q(x)\cdot (x-2) \, = \, P(x)$:

$$\begin{array}{rclc} Q(x) \cdot (x - 2) & = & (a\,x^2 + b\,x + c)\cdot (x - 2) & = \\ & = & a\,x^3 - 2\,a\,x^2 + b\,x^2 - 2\,b\,x + c\,x - 2\,c & = \\ & = & a\,x^3 + (-2\,a + b)\,x^2 + (-2\,b + c)\,x - 2\,c & = \\ & = & a \cdot x^3 + (-2\,a + b) \cdot x^2 + (-2\,b + c) \cdot x - 2\,c \cdot x^0 & \\ P(x) & = & 1 \cdot x^3 + \quad\;\;\;\;4 \quad\;\; \cdot x^2 + \quad\;\;\;\,1 \quad\;\; \cdot x - 26 \cdot x^0 \end{array}$$

Koefficienterna till polynomen $\; Q(x) \cdot (x - 2) \;$ och $\; P(x) \;$ jämförs med varandra:

Jämförelse av koefficienterna till $x^3$-termen ger: $\qquad\qquad a = 1$

Jämförelse av koefficienterna till $x^2$-termen ger:

$$\begin{align} -2\,a + b & = 4 \\ -2\cdot 1 + b & = 4 \\ - 2 + b & = 4 \\ b & = 6 \\ \end{align}$$

Jämförelse av koefficienterna till $x^1$-termen ger:

$$\begin{align} -2\,b + c & = 1 \\ -2\cdot 6 + c & = 1 \\ -12 + c & = 1 \\ c & = 13 \\ \end{align}$$

Jämförelse av koefficienterna till $x^0 \,$-termen bekräftar värdet på $c \,$:

$$\begin{align} - 2\,c & = - 26 \\ c & = 13 \\ \end{align}$$

Vi får $a = 1\, , \, b = 6\,$ och $c = 13\,$ och därmed: $\quad Q(x) = x^2 + 6 \, x + 13$

Alltså är: $\qquad (x^3 + 4\,x^2 + x - 26) \; / \; (x-2) \; = \; x^2 + 6 \, x + 13$

Övningar 4417-4426

Copyright © 2022 TechPages AB. All Rights Reserved.