Skillnad mellan versioner av "4.16 Faktorsatsen"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 21: | Rad 21: | ||
| − | + | = <b><span style="color:#931136">Regler om en funktions växande och avtagande</span></b> = | |
| − | + | <big> | |
Det är <b><span style="color:red">derivatans tecken</span></b> (<math> \,+\, </math> eller <math> \,-\, </math>) som avgör om en funktion är växande eller avtagande. | Det är <b><span style="color:red">derivatans tecken</span></b> (<math> \,+\, </math> eller <math> \,-\, </math>) som avgör om en funktion är växande eller avtagande. | ||
<div class="border-divblue"> | <div class="border-divblue"> | ||
| Rad 53: | Rad 53: | ||
</table> | </table> | ||
</div> | </div> | ||
| − | + | </big> | |
Versionen från 28 mars 2022 kl. 07.41
IND_VAL: v14 II, tor kl 14.40-15.50, sal 2. Övningar 4429-4440.
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
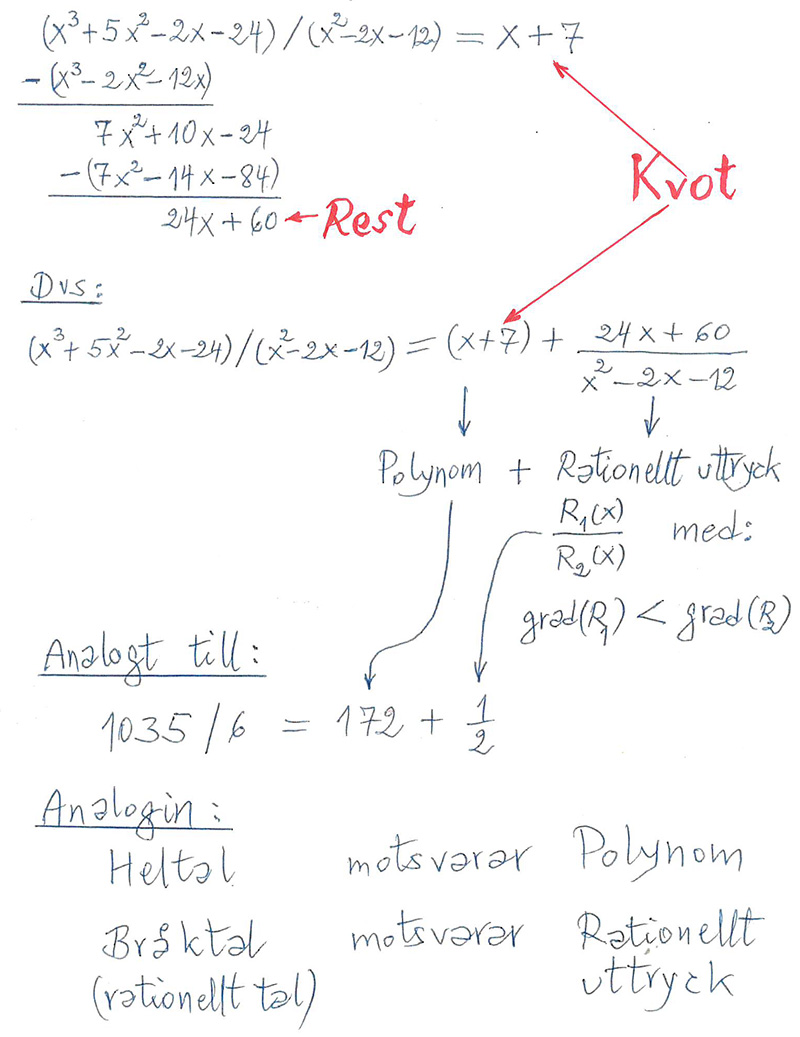
Manuell division av polynom med rest \( \; \neq 0 \)
Regler om en funktions växande och avtagande
Det är derivatans tecken (\( \,+\, \) eller \( \,-\, \)) som avgör om en funktion är växande eller avtagande.
| Funktionen \( \; y \, = \, f(x) \; \) är växande för \( \; x = a \; \) om derivatan \( \; f\,'(a) \, {\bf {\color{Red} >}} \, 0 \;. \)
Funktionen \( \; y \, = \, f(x) \; \) är avtagande för \( \; x = a \; \) om derivatan \( \; f\,'(a) \, {\bf {\color{Red} <}} \, 0 \;. \)
|
Copyright © 2022 TechPages AB. All Rights Reserved.