Skillnad mellan versioner av "4.7 Visualiseringar i det komplexa talplanet"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 14: | Rad 14: | ||
| − | = <b><span style="color:#931136"> | + | = <b><span style="color:#931136">Linjer och ytor</span></b> = |
<div class="ovnE"> | <div class="ovnE"> | ||
=== <b><span style="color:#931136">Det komplexa talplanet</span></b> === | === <b><span style="color:#931136">Det komplexa talplanet</span></b> === | ||
Versionen från 16 februari 2022 kl. 13.35
IND_VAL: v8 I, tis kl 11.15-12.20, sal 10. Övningar 4212-4216.
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
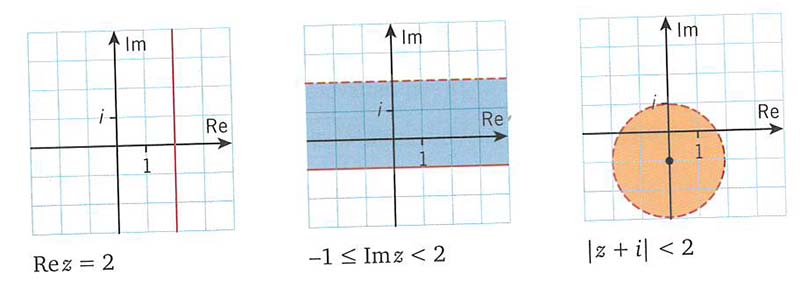
Linjer och ytor
Det komplexa talplanet
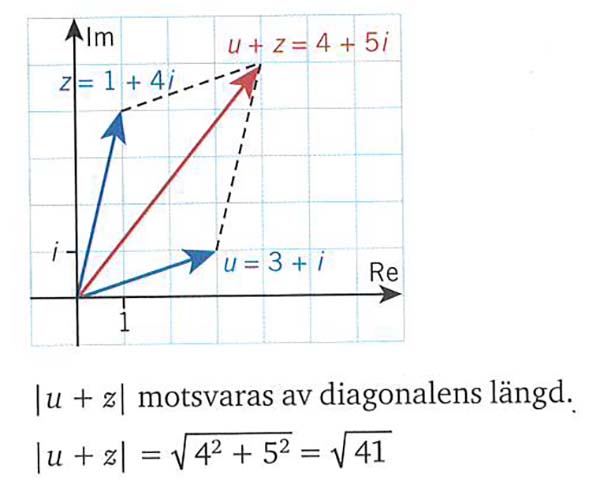
Addition av komplexa tal som addition av vektorer
Summan = diagonalen i parallellogram som spänns upp av vektorerna
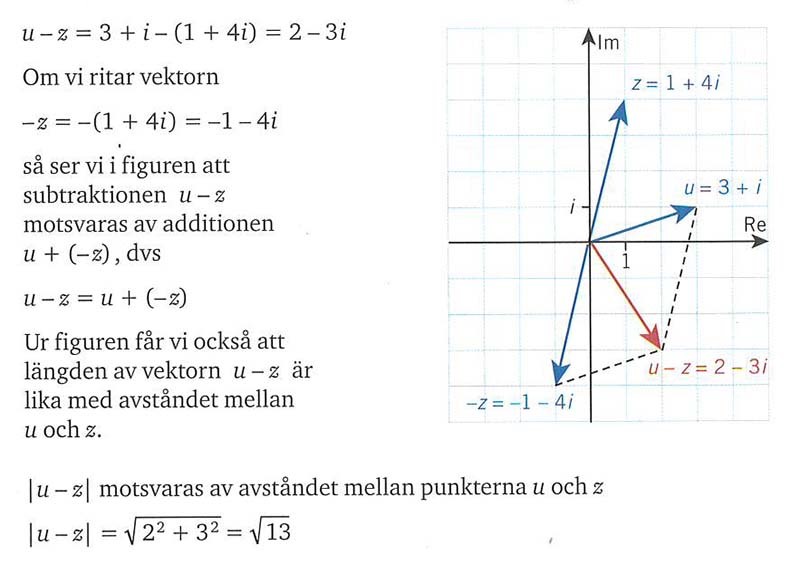
Subtraktion av komplexa tal som subtraktion av vektorer
u = 3 + i z = 1 + 4i
Differensen u - z bildas som summan u + (-z)
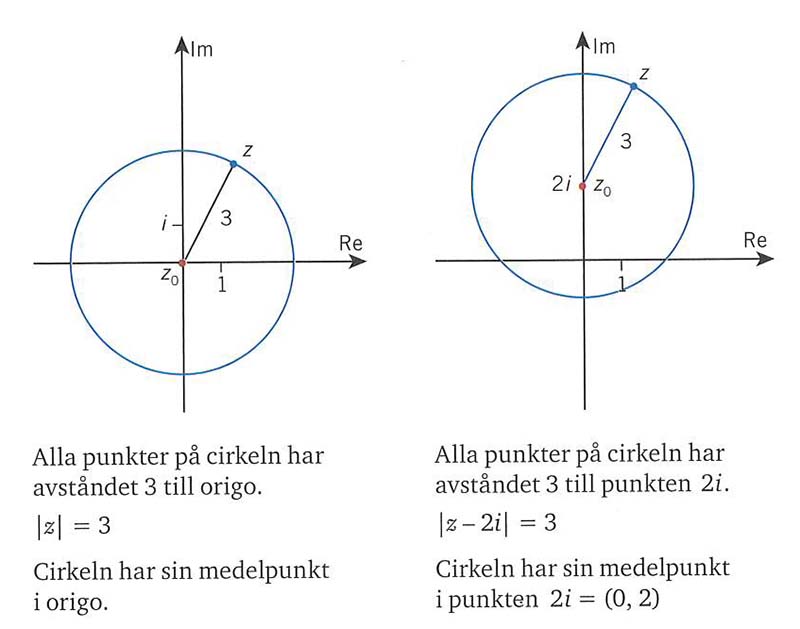
Cirkelns ekvation
Cirkel = Mängden av alla punkter \( \, z \, \) som har samma avstånd från medelpunkten \( \, z_0 \)
Avståndet mellan \( \, z \, \) och \( \, z_0 \; \) är \( \; | \, z - z_0 \, | \; \implies \; \)Cirkelns ekvation: \( \; | \, z - z_0 \, | \; = \; r\)
Ex.:
Copyright © 2022 TechPages AB. All Rights Reserved.
