Skillnad mellan versioner av "1.6 Trigonometriska ekvationer"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 24: | Rad 24: | ||
| − | + | = <b><span style="color:#931136">Slutsatser</span></b> = | |
| + | <big> | ||
<div class="border-divblue">En <b><span style="color:red">sinus</span></b>ekvation har i intervallet <math> \, 0^\circ \leq v \leq 180^\circ \, </math> alltid <b><span style="color:red">två</span></b> lösningar.<br><br> | <div class="border-divblue">En <b><span style="color:red">sinus</span></b>ekvation har i intervallet <math> \, 0^\circ \leq v \leq 180^\circ \, </math> alltid <b><span style="color:red">två</span></b> lösningar.<br><br> | ||
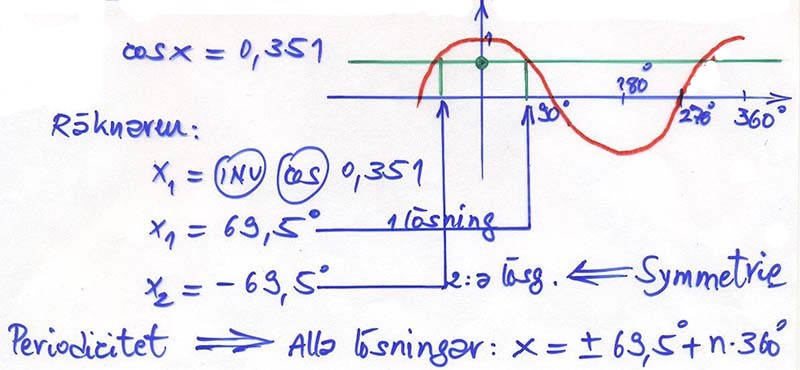
En <b><span style="color:red">cosinus</span></b>ekvation har i intervallet <math> \, 0^\circ \leq v \leq 180^\circ \, </math> <b><span style="color:red">endast en</span></b> lösning.</div> | En <b><span style="color:red">cosinus</span></b>ekvation har i intervallet <math> \, 0^\circ \leq v \leq 180^\circ \, </math> <b><span style="color:red">endast en</span></b> lösning.</div> | ||
Nuvarande version från 25 augusti 2025 kl. 13.31
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
Exempel sinusekvation
Exempel cosinusekvation
Slutsatser
En sinusekvation har i intervallet \( \, 0^\circ \leq v \leq 180^\circ \, \) alltid två lösningar.
En cosinusekvation har i intervallet \( \, 0^\circ \leq v \leq 180^\circ \, \) endast en lösning.
En cosinusekvation har i intervallet \( \, 0^\circ \leq v \leq 180^\circ \, \) endast en lösning.
Copyright © 2025 Lieta AB. All Rights Reserved.