Skillnad mellan versioner av "4.15 Polynomdivision"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 23: | Rad 23: | ||
== <b><span style="color:#931136">Alternativ metod för polynomdivision: Jämförelse av koefficienter</span></b> == | == <b><span style="color:#931136">Alternativ metod för polynomdivision: Jämförelse av koefficienter</span></b> == | ||
| − | <div class=" | + | <div class="ovnC"> |
'''Uppgift:''' <math> \qquad </math> Utför polynomdivisionen <math> \quad (x^3 + 4\,x^2 + x - 26) \; / \; (x-2) </math> | '''Uppgift:''' <math> \qquad </math> Utför polynomdivisionen <math> \quad (x^3 + 4\,x^2 + x - 26) \; / \; (x-2) </math> | ||
Versionen från 25 mars 2022 kl. 10.40
IND_VAL: v13 I, tis kl 11.15-12.20, sal 10. Övningar 4417-4426.
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
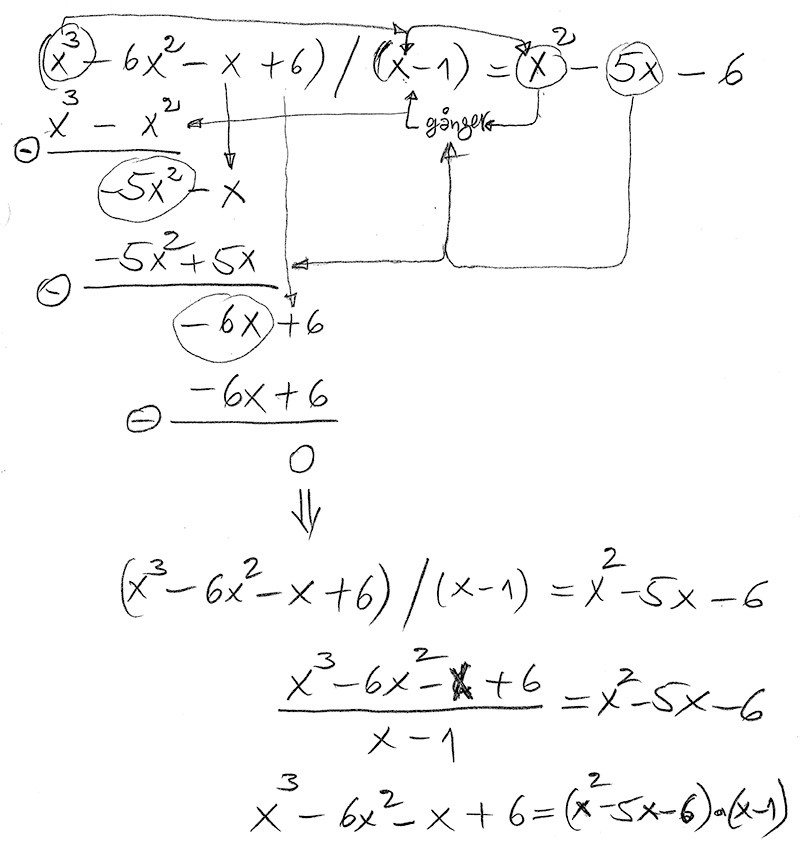
Dividera \( \; x^3 - 6 x^2 - x + 6 \; \) med \( \; x - 1 \)
Alternativ metod för polynomdivision: Jämförelse av koefficienter
Uppgift: \( \qquad \) Utför polynomdivisionen \( \quad (x^3 + 4\,x^2 + x - 26) \; / \; (x-2) \)
En annan formulering av uppgiften är:
Hitta ett 2:a gradspolynom \( \, Q(x)\, \) så att \( \, Q(x)\cdot (x-2) = (x^3 + 4\,x^2 + x - 26) \)
Lösning:
Vi inför beteckningen: \( \quad\;\;\, P(x) = x^3 + 4\,x^2 + x - 26 \).
Det 2:a gradspolynomet \( Q(x)\, \) kan skrivas så här: \( \qquad Q(x) = a\,x^2 + b\,x + c \)
Vi bestämmer koefficienterna \( a\, , \, b\, \) och \( c\, \) så att \( \; Q(x)\cdot (x-2) \, = \, P(x) \):
- \[\begin{array}{rclc} Q(x) \cdot (x - 2) & = & (a\,x^2 + b\,x + c)\cdot (x - 2) & = \\ & = & a\,x^3 - 2\,a\,x^2 + b\,x^2 - 2\,b\,x + c\,x - 2\,c & = \\ & = & a\,x^3 + (-2\,a + b)\,x^2 + (-2\,b + c)\,x - 2\,c & = \\ & = & a \cdot x^3 + (-2\,a + b) \cdot x^2 + (-2\,b + c) \cdot x - 2\,c \cdot x^0 & \\ P(x) & = & 1 \cdot x^3 + \quad\;\;\;\;4 \quad\;\; \cdot x^2 + \quad\;\;\;\,1 \quad\;\; \cdot x - 26 \cdot x^0 \end{array} \]
Jämförelse av koefficienterna till \( x^3 \)-termen ger:
- \[ a = 1 \]
Jämförelse av koefficienterna till \( x^2 \)-termen ger:
- \[\begin{align} -2\,a + b & = 4 \\ -2\cdot 1 + b & = 4 \\ - 2 + b & = 4 \\ b & = 6 \\ \end{align} \]
Jämförelse av koefficienterna till \( x^1 \)-termen ger:
- \[\begin{align} -2\,b + c & = 1 \\ -2\cdot 6 + c & = 1 \\ -12 + c & = 1 \\ c & = 13 \\ \end{align} \]
Jämförelse av koefficienterna till \( x^0 \, \)-termen bekräftar värdet på \( c \, \):
- \[\begin{align} - 2\,c & = - 26 \\ c & = 13 \\ \end{align} \]
Vi får \( a = 1\, , \, b = 6\, \) och \( c = 13\, \) och därmed: \( \quad Q(x) = x^2 + 6 \, x + 13 \)
Alltså är: \( \qquad (x^3 + 4\,x^2 + x - 26) \; / \; (x-2) \; = \; x^2 + 6 \, x + 13\)
Anmärkningar
- Polynomdivision kan även genomföras genom att direkt dividera polynomen med varandra, se Matte 4-kursen. Den är mer generell därför att den kan användas också för andra problem, t.ex. faktorisering av polynom eller lösning av differentialekvationer. Jämförelse av koefficienter ger mer insikt i polynomens struktur.
- Ett annat namn för jämförelse av koefficienter är Metoden med obestämda koefficienter (eng.: Method of undetermined coefficients). Med obestämda koefficienter menar man den ansats som man i början gör med obestämda koefficienter som man sedan bestämmer under metodens gång.
- Ytterligare ett namn för samma metod är Ansatsmetoden.
Copyright © 2022 TechPages AB. All Rights Reserved.