Skillnad mellan versioner av "4.15 Polynomdivision"

Från Mathonline
Hoppa till: navigering, sök
m
m
 
(20 mellanliggande versioner av samma användare visas inte)
Rad 1: Rad 1:
 
__NOTOC__
 
__NOTOC__
−
IND_VAL: v13 I, tis kl 11.15-12.20, sal 10. [[Media: 4_15_Polynomdivision_Ovn.pdf|<b><span style="color:blue">Övningar 4417-4426</span></b>]].
 
−
 
−
 
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" | &nbsp;
 
| style="border-bottom:1px solid #797979" width="5px" | &nbsp;
Rad 9: Rad 6:
 
{{Not selected tab|[[Media: 4_15_Polynomdiv_Ovn.pdf|Övningar]]}}
 
{{Not selected tab|[[Media: 4_15_Polynomdiv_Ovn.pdf|Övningar]]}}
 
{{Not selected tab|[[Media: 4_15_Polynomdiv_Facit.pdf|Facit]]}}
 
{{Not selected tab|[[Media: 4_15_Polynomdiv_Facit.pdf|Facit]]}}
−
{{Not selected tab|[[4.15 Polynomdivision|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
+
{{Not selected tab|[[4.16 Faktorsatsen|Nästa avsnitt&nbsp;&nbsp;>> ]]}}
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
  
  
−
= <b><span style="color:#931136">Dividera <math> \; x^3 - 6 x^2 - x + 6 \; </math> med <math> \; x - 1 </math></span></b> =
+
= <b><span style="color:#931136">Manuell division av heltal med rest <math> \; \neq 0 </math></span></b> =
 +
<div class="ovnE">
 +
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_15_Man_div_heltal_800.jpg]] </div>
 +
</div>
  
  
 +
= <b><span style="color:#931136">Manuell division av heltal utan rest</span></b> =
 
<div class="ovnE">
 
<div class="ovnE">
 +
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_15_Man_div_heltal_Rest_0.jpg]] </div>
 +
</div>
 +
 +
 +
= <b><span style="color:#931136">Manuell division av polynom utan rest</span></b> =
 +
<div class="ovnC">
 +
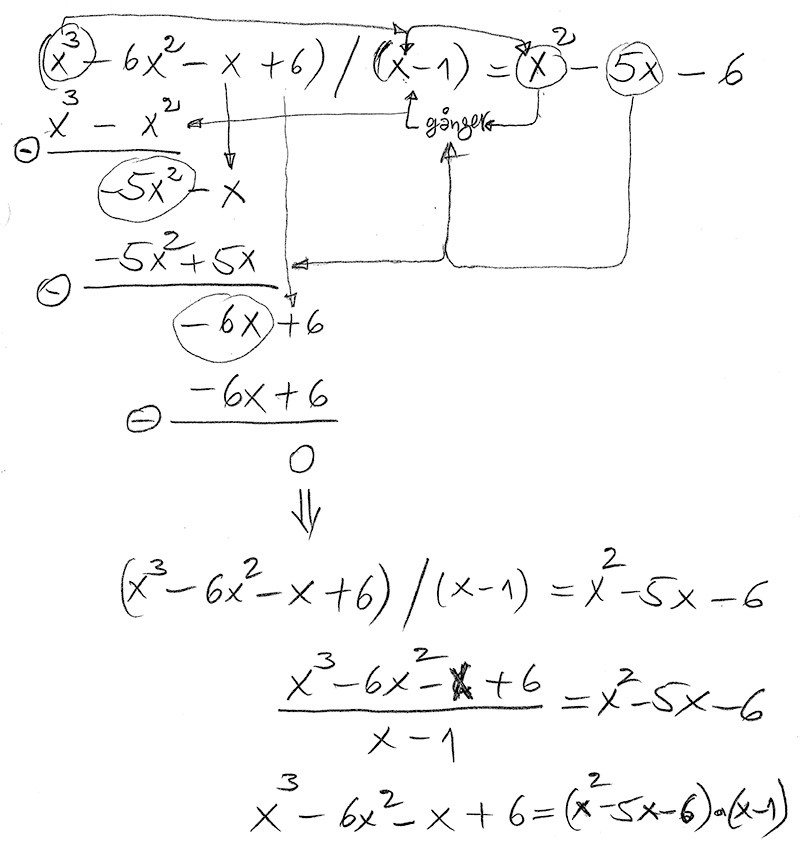
== <b><span style="color:#931136">Dividera <math> \; x^3 - 6 x^2 - x + 6 \; </math> med <math> \; x - 1 </math></span></b> ==
 
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_15_Polynomdiva.jpg]] </div>
 
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_15_Polynomdiva.jpg]] </div>
 
</div>
 
</div>
  
−
+++
 
  
−
= <small><b><span style="color:#931136">Vietas formler</span></b></small> =
+
= <b><span style="color:#931136">Jämförelse av koefficienter, en alternativ metod för polynomdivision utan rest</span></b> =
 +
<div class="ovnA">
 
<big>
 
<big>
−
<div class="border-divblue">
+
'''Uppgift:''' <math> \qquad </math> Utför polynomdivisionen <math> \quad (x^3 + 4\,x^2 + x - 26) \; / \; (x-2) </math>
−
Om 2:gradsekvationen <math> \; x^2 + p\,x + q \; = \; 0 \; </math> har lösningarna
+
  
−
<math> x_1\, </math> och <math> x_2\, </math> så gäller<span style="color:black">:</span> <math> \qquad \boxed{\begin{align} x_1  +  x_2 & = -p  \\
+
En annan formulering av uppgiften är:
−
                        x_1 \cdot x_2 & = q
+
−
          \end{align}} </math>
+
−
</div>
+
−
</big>
+
  
 +
Hitta ett 2:a gradspolynom <math> \, Q(x)\, </math> så att <math> \, Q(x)\cdot (x-2) = (x^3 + 4\,x^2 + x - 26) </math>
  
−
= <b><span style="color:#931136">Den konstanta termen saknas: Nollproduktmetoden</span></b> =
+
'''Lösning:'''
−
<div class="ovnE">
+
−
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 3_3_Nollproduktmetoden.jpg]] </div>
+
−
</div>
+
  
 +
Vi inför beteckningen<span>:</span> <math> \quad\;\;\, P(x) = x^3 + 4\,x^2 + x - 26 </math>.
  
−
= <b><span style="color:#931136">Den linjära termen saknas: Kvadratrotsmetoden</span></b> =
+
<math> Q(x)\, </math> kan skrivas så här (Ansats)<span>:</span> <math> \qquad Q(x) = a\,x^2 + b\,x + c </math>  
−
<div class="ovnE">
+
−
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 3_3_Kvadratrotsmetodena.jpg]] </div>
+
−
</div>
+
  
 +
Vi bestämmer koefficienterna <math> a\, , \, b\, </math> och <math> c\, </math> så att <math> \; Q(x)\cdot (x-2) \, = \, P(x) </math><span style="color:black">:</span>
  
−
= <b><span style="color:#931136">Användning av Eulers formel</span></b> =
+
::<math>\begin{array}{rclc} Q(x) \cdot (x - 2) & = & (a\,x^2 + b\,x + c)\cdot (x - 2) & = \\
−
<div class="ovnA">
+
                                              & = & a\,x^3 - 2\,a\,x^2 + b\,x^2 - 2\,b\,x + c\,x - 2\,c                      & = \\
−
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_14_Polynomekv_1.jpg]]</div>
+
                                              & = & a\,x^3 + (-2\,a + b)\,x^2 + (-2\,b + c)\,x - 2\,c                        & = \\
 +
                                              & = & a \cdot x^3 + (-2\,a + b) \cdot x^2 + (-2\,b + c) \cdot x - 2\,c \cdot x^0 &  \\
 +
                            P(x)              & = & 1 \cdot x^3  + \quad\;\;\;\;4 \quad\;\; \cdot x^2  + \quad\;\;\;\,1 \quad\;\; \cdot x - 26 \cdot x^0
 +
\end{array} </math>
  
 +
Koefficienterna till polynomen <math> \; Q(x) \cdot (x - 2) \; </math> och <math> \; P(x) \; </math> jämförs med varandra:
  
−
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_14_Polynomekv_2.jpg]]</div>
+
Jämförelse av koefficienterna till <math> x^3 </math>-termen ger<span>:</span> <math> \qquad\qquad a = 1 </math>
−
</div>
+
  
 +
Jämförelse av koefficienterna till <math> x^2 </math>-termen ger<span style="color:black">:</span>
  
−
= <b><span style="color:#931136">Att dra (3:e) roten ur ett komplext tal: Använd Euler</span></b> =
+
::<math>\begin{align} -2\,a + b     & = 4  \\
−
<div class="ovnE">
+
                      -2\cdot 1 + b & = 4  \\
−
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_14_Polynomekv_3a.jpg]]</div>
+
                            - 2 + b & = 4  \\
−
</div>
+
                                  b & = 6  \\
 +
        \end{align} </math>
  
 +
Jämförelse av koefficienterna till <math> x^1 </math>-termen ger<span style="color:black">:</span>
  
−
= <b><span style="color:#931136">Repetition: Konjugatets egenskaper</span></b> =
+
::<math>\begin{align} -2\,b + c & = 1  \\
−
<div class="ovnC">
+
                  -2\cdot 6 + c & = 1  \\
−
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: 4_2_Komplexa_tal_2.jpg]]
+
                        -12 + c & = 1  \\
−
</div>
+
                              c & = 13  \\
 +
        \end{align} </math>
 +
 
 +
Jämförelse av koefficienterna till <math> x^0 \, </math>-termen bekräftar värdet på <math> c \, </math><span style="color:black">:</span>
 +
 
 +
::<math>\begin{align} - 2\,c & = - 26  \\
 +
                          c & = 13    \\
 +
        \end{align} </math>
 +
 
 +
Vi får <math> a = 1\, , \, b = 6\, </math> och <math> c = 13\, </math> och därmed<span style="color:black">:</span> <math> \quad Q(x) = x^2 + 6 \, x + 13 </math>
 +
 
 +
 
 +
Alltså är<span style="color:black">:</span> <math> \qquad (x^3 + 4\,x^2 + x - 26) \; / \; (x-2) \; = \; x^2 + 6 \, x + 13</math>
 +
</big>
 
</div>
 
</div>
 +
 +
 +
[[Media: 4_15_Polynomdiv_Ovn.pdf|<b><span style="color:blue">Övningar 4417-4426</span></b>]]
  
  

Nuvarande version från 2 april 2025 kl. 07.49

        <<  Förra avsnitt          Genomgång          Övningar          Facit          Nästa avsnitt  >>      


Manuell division av heltal med rest \( \; \neq 0 \)

4 15 Man div heltal 800.jpg


Manuell division av heltal utan rest

4 15 Man div heltal Rest 0.jpg


Manuell division av polynom utan rest

Dividera \( \; x^3 - 6 x^2 - x + 6 \; \) med \( \; x - 1 \)

4 15 Polynomdiva.jpg


Jämförelse av koefficienter, en alternativ metod för polynomdivision utan rest

Uppgift: \( \qquad \) Utför polynomdivisionen \( \quad (x^3 + 4\,x^2 + x - 26) \; / \; (x-2) \)

En annan formulering av uppgiften är:

Hitta ett 2:a gradspolynom \( \, Q(x)\, \) så att \( \, Q(x)\cdot (x-2) = (x^3 + 4\,x^2 + x - 26) \)

Lösning:

Vi inför beteckningen: \( \quad\;\;\, P(x) = x^3 + 4\,x^2 + x - 26 \).

\( Q(x)\, \) kan skrivas så här (Ansats): \( \qquad Q(x) = a\,x^2 + b\,x + c \)

Vi bestämmer koefficienterna \( a\, , \, b\, \) och \( c\, \) så att \( \; Q(x)\cdot (x-2) \, = \, P(x) \):

\[\begin{array}{rclc} Q(x) \cdot (x - 2) & = & (a\,x^2 + b\,x + c)\cdot (x - 2) & = \\ & = & a\,x^3 - 2\,a\,x^2 + b\,x^2 - 2\,b\,x + c\,x - 2\,c & = \\ & = & a\,x^3 + (-2\,a + b)\,x^2 + (-2\,b + c)\,x - 2\,c & = \\ & = & a \cdot x^3 + (-2\,a + b) \cdot x^2 + (-2\,b + c) \cdot x - 2\,c \cdot x^0 & \\ P(x) & = & 1 \cdot x^3 + \quad\;\;\;\;4 \quad\;\; \cdot x^2 + \quad\;\;\;\,1 \quad\;\; \cdot x - 26 \cdot x^0 \end{array} \]

Koefficienterna till polynomen \( \; Q(x) \cdot (x - 2) \; \) och \( \; P(x) \; \) jämförs med varandra:

Jämförelse av koefficienterna till \( x^3 \)-termen ger: \( \qquad\qquad a = 1 \)

Jämförelse av koefficienterna till \( x^2 \)-termen ger:

\[\begin{align} -2\,a + b & = 4 \\ -2\cdot 1 + b & = 4 \\ - 2 + b & = 4 \\ b & = 6 \\ \end{align} \]

Jämförelse av koefficienterna till \( x^1 \)-termen ger:

\[\begin{align} -2\,b + c & = 1 \\ -2\cdot 6 + c & = 1 \\ -12 + c & = 1 \\ c & = 13 \\ \end{align} \]

Jämförelse av koefficienterna till \( x^0 \, \)-termen bekräftar värdet på \( c \, \):

\[\begin{align} - 2\,c & = - 26 \\ c & = 13 \\ \end{align} \]

Vi får \( a = 1\, , \, b = 6\, \) och \( c = 13\, \) och därmed: \( \quad Q(x) = x^2 + 6 \, x + 13 \)


Alltså är: \( \qquad (x^3 + 4\,x^2 + x - 26) \; / \; (x-2) \; = \; x^2 + 6 \, x + 13\)


Övningar 4417-4426









Copyright © 2022 TechPages AB. All Rights Reserved.

Hämtad från "https://matte4.mathonline.se/index.php?title=4.15_Polynomdivision&oldid=11389"