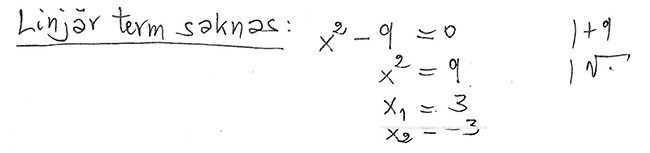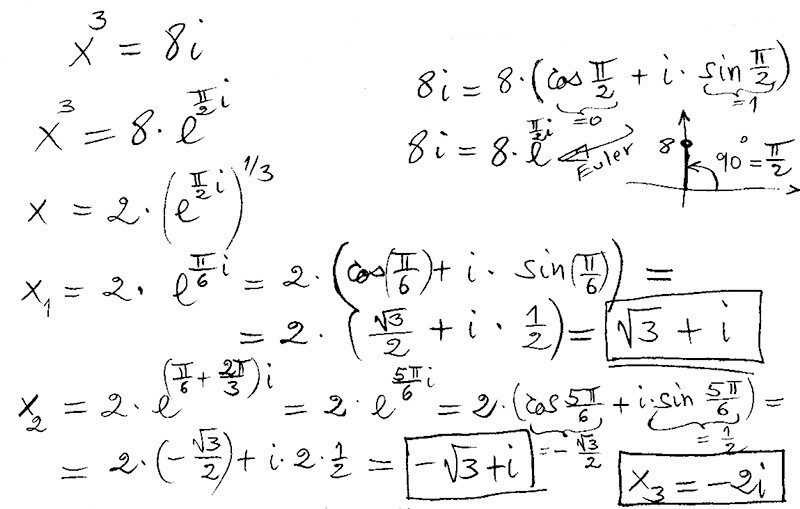Skillnad mellan versioner av "4.14 Polynomekvationer"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 3: | Rad 3: | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
{{Not selected tab|[[4.13 Eulers formel| << Förra avsnitt]]}} | {{Not selected tab|[[4.13 Eulers formel| << Förra avsnitt]]}} | ||
| − | {{Selected tab|[[4.14 Polynomekvationer|Genomgång | + | {{Selected tab|[[4.14 Polynomekvationer|<span style="font-weight:lighter">Genomgång</span>]}} |
{{Not selected tab|[[Media: 4_14_Polynomekv_Ovn.pdf|Övningar]]}} | {{Not selected tab|[[Media: 4_14_Polynomekv_Ovn.pdf|Övningar]]}} | ||
{{Not selected tab|[[Media: 4_14_Polynomekv_Facit.pdf|Facit]]}} | {{Not selected tab|[[Media: 4_14_Polynomekv_Facit.pdf|Facit]]}} | ||
Versionen från 12 november 2025 kl. 13.54
| << Förra avsnitt |
{{Selected tab|[[4.14 Polynomekvationer|Genomgång]}} |
Övningar | Facit | Nästa avsnitt >> |
Orientering om andragradsekvationer
Vietas formler
Om 2:gradsekvationen \( \; x^2 + p\,x + q \; = \; 0 \; \) har lösningarna
\( x_1\, \) och \( x_2\, \) så gäller: \( \qquad \boxed{\begin{align} x_1 + x_2 & = -p \\ x_1 \cdot x_2 & = q \end{align}} \)
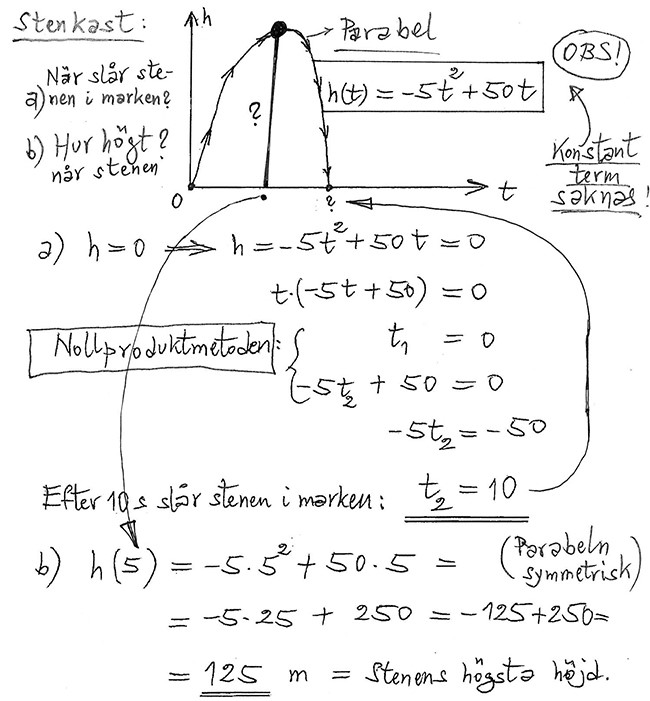
Den konstanta termen saknas: Nollproduktmetoden
Den linjära termen saknas: Kvadratrotsmetoden
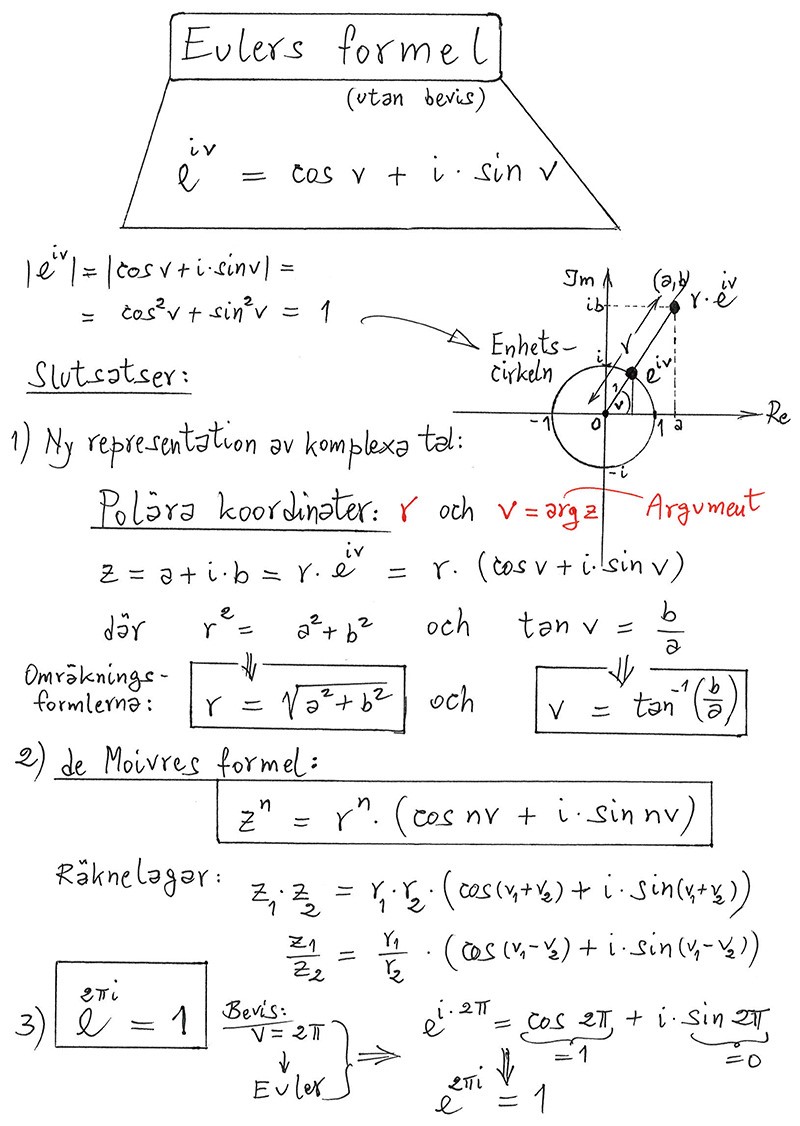
Användning av Eulers formel
Att dra (3:e) roten ur ett komplext tal: Använd Euler
Repetition: Konjugatets egenskaper
Copyright © 2022 TechPages AB. All Rights Reserved.