4.10 Avläsa och rita i det komplexa talplanet
Från Mathonline
Version från den 16 mars 2025 kl. 10.50 av Taifun (Diskussion | bidrag)
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
Sammanfattning
Komplext tal \( \qquad z \, = \, a + b \, i \quad = \quad r \, (cos\,v + i \, sin\,v) \)
Cartesiska koordinater: \( \qquad a, \quad b \)
Polära koordinater:
\( r \; = \; | z | \; = \; \) Absolutbelopp \( \qquad\qquad v \; = \; \arg z \; = \; \) Argument
\( r \; = \; | z | \; = \; \sqrt{a^2 + b^2} \)
\( \tan v \, = \, b/a \; \implies \; v \, = \, \tan^{-1} (b/a) \)
Omvänt: \( \quad a \, = \, r \, \cos v \qquad b \, = \, r \, \sin v \)
Regler för multiplikation och division i polär form:
1. Multiplicera absolutbeloppen och addera argumenten.
2. Dividera absolutbeloppen och subtrahera argumenten.
Avläsa och rita
Tre uppgifter:
1) Läs av koordinaterna av ett komplext tal (cartesiska eller polära) från grafen.
2) Omvänt: Rita in koordinaterna (cartesiska eller polära) i grafen.
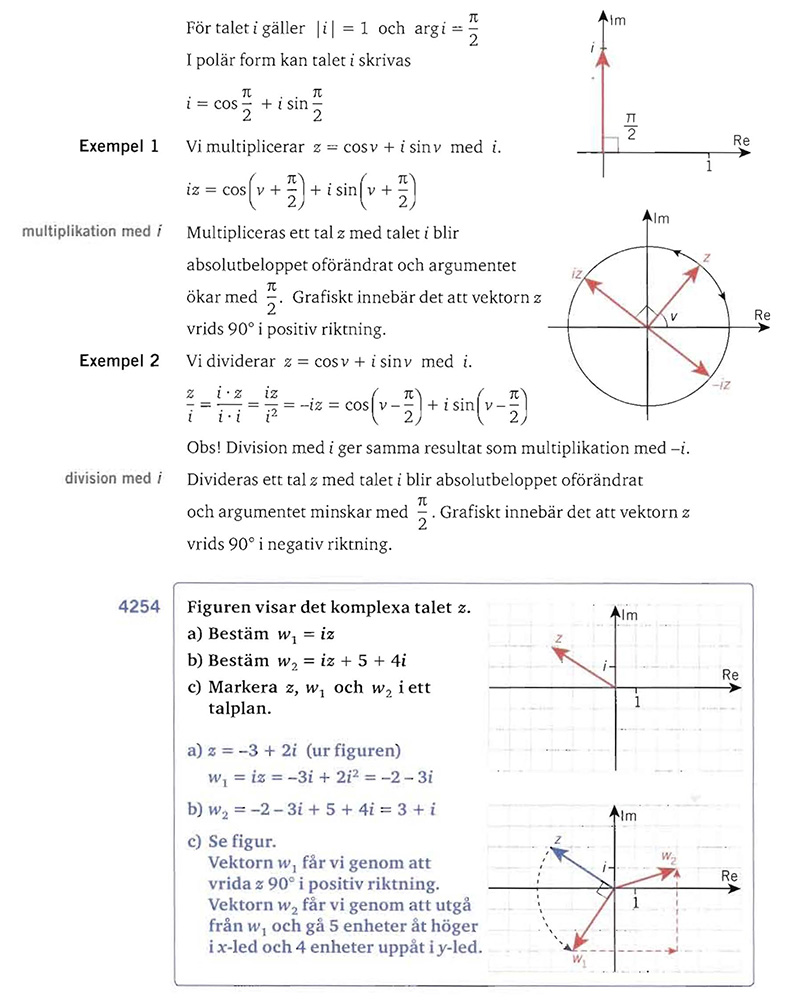
3) Vad händer grafiskt vid multiplikation/division med \(i\) resp. \(-i\) ?
Copyright © 2022 TechPages AB. All Rights Reserved.