Versionen från 12 december 2020 kl. 18.35

Genomgång

Övningar

Vad är rekursion?

Ordet rekursion kommer från det latinska recurrere som betyder att köra igen. Dvs:

Man återvänder till något som man redan gjort en gång - en upprepning av ett känt förlopp, men:

under nya förutsättningar, med nya premisser, med nya parametrar.

Rekursion är ett koncept som ofta används i datoriserad problemlösning genom successiv upprepning.

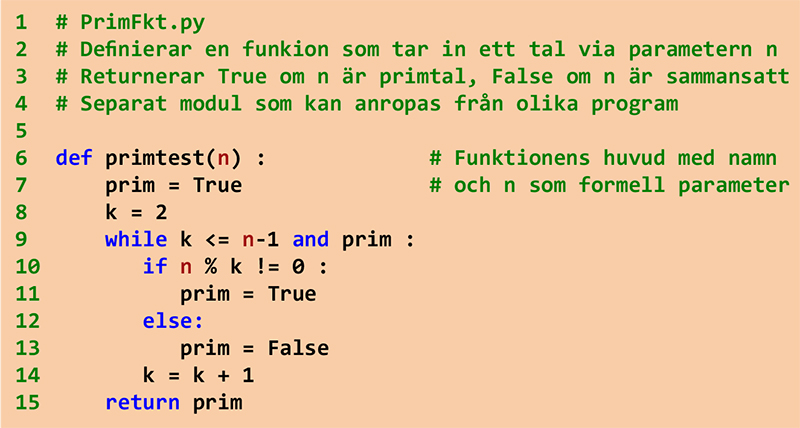
Kan användas som modul i alla program för att avgöra om ett tal är primtal.

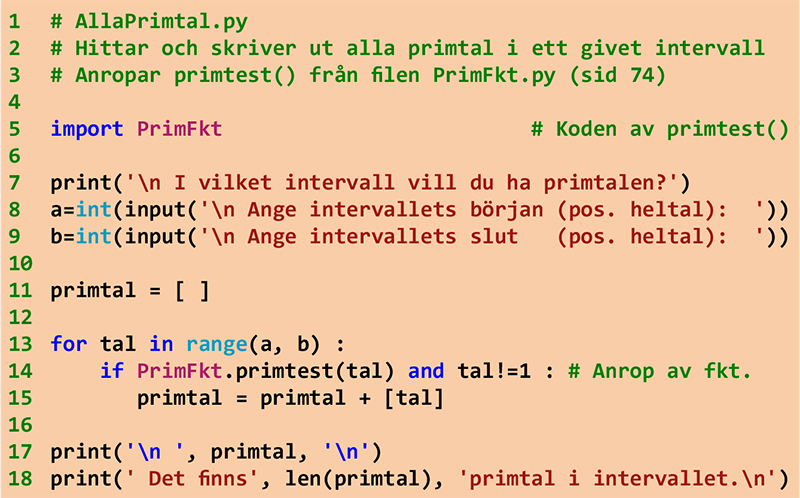
Vi använder modulen i programmet nedan för att hitta alla primtal i ett intervall.

@@ Rad 9: / Rad 9: @@
-= <b><span style="color:#931136">Betydelsen</span></b> =
+= <b><span style="color:#931136">Vad är rekursion?</span></b> =
 <div class="ovnE">
 <big><big>Ordet <b><span style="color:red">rekursion</span></b> kommer från det latinska <i>recurrere</i> som betyder <b><span style="color:red">att köra igen</span></b>. Dvs:
-Man återvänder till något som man redan gjort en gång - en upprepning av ett känt förlopp.
+Man återvänder till något som man redan gjort en gång - en upprepning av ett känt förlopp, men:
+under nya förutsättningar, med nya premisser, med nya parametrar.
+Rekursion är ett koncept som ofta används i datoriserad problemlösning genom successiv upprepning.
 </big></big>
 </div>