Skillnad mellan versioner av "While-satsen i Python"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 29: | Rad 29: | ||
<big><big> | <big><big> | ||
| − | * Några enkla manuella | + | * Några enkla manuella experiment visar: |
Slutresultatet blir 1 oavsett startvärde. Testa själva! | Slutresultatet blir 1 oavsett startvärde. Testa själva! | ||
| − | * | + | * Med ett datorprogram skulle man kunna testa mer omfattande: OBS! Fortfarande inget bevis! |
* Även kallat (3n+1)-problemet eller Collatz-förmodan efter den tyske matematikern Lothar Collatz (1910-1990) | * Även kallat (3n+1)-problemet eller Collatz-förmodan efter den tyske matematikern Lothar Collatz (1910-1990) | ||
Versionen från 10 november 2020 kl. 12.36
| << Lektion 10 | Genomgång | for-satsen >> | Hantering av slumptal >> | Övningar >> |
Problemet
1) Tänk dig ett positivt heltal.
2) Om talet är jämnt dela det med 2.
3) Om talet är udda multiplicera det med 3 och addera 1.
4) Gör samma sak med resultatet, dvs:
Gå tillbaka till 2) och upprepa 2)-4).
Vad blir slutresultatet?
- Några enkla manuella experiment visar:
Slutresultatet blir 1 oavsett startvärde. Testa själva!
- Med ett datorprogram skulle man kunna testa mer omfattande: OBS! Fortfarande inget bevis!
- Även kallat (3n+1)-problemet eller Collatz-förmodan efter den tyske matematikern Lothar Collatz (1910-1990)
som ställde upp problemet. Collatz var Professor för Tillämpad Matematik vid Hamburgs Universitet på 60-talet.
- Ett matematiskt bevis saknas.
Pseudokoden
Programmet
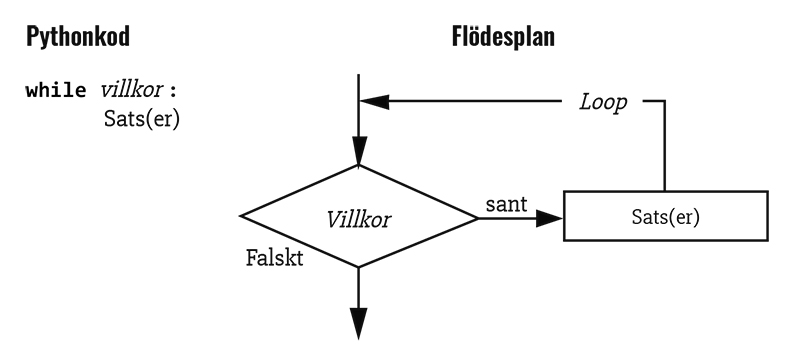
while-satsen, en loop
Läs mer om while-satsen.
Copyright © 2020 TechPages AB. All Rights Reserved.