Skillnad mellan versioner av "1.10 Ekvationen för en sinusformad kurva"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 10: | Rad 10: | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
{{Not selected tab|[[1.9 Förskjutade trigonometriska kurvor|<< Förra avsnitt]]}} | {{Not selected tab|[[1.9 Förskjutade trigonometriska kurvor|<< Förra avsnitt]]}} | ||
| − | {{Selected tab|[[1.10 Ekvationen för en sinusformad kurva|Genomgång]]}} | + | {{Selected tab|[[1.10 Ekvationen för en sinusformad kurva|<span style="font-weight:lighter">Genomgång</span>]]}} |
{{Not selected tab|[[Media: 2_3_Ekv_sinusformad_kurva_Ovn.pdf|Övningar]]}} | {{Not selected tab|[[Media: 2_3_Ekv_sinusformad_kurva_Ovn.pdf|Övningar]]}} | ||
{{Not selected tab|[[Media: 2_3_Ekv_sinusformad_kurva_Facit.pdf|Facit]]}} | {{Not selected tab|[[Media: 2_3_Ekv_sinusformad_kurva_Facit.pdf|Facit]]}} | ||
| Rad 20: | Rad 20: | ||
= <b><span style="color:#931136">Kombinera amplitud, frekvens och förskjutning</span></b> = | = <b><span style="color:#931136">Kombinera amplitud, frekvens och förskjutning</span></b> = | ||
<div class="ovnE"> | <div class="ovnE"> | ||
| − | === | + | === <span style="color:#931136">Generellt: y = A sin k(x-b) + d</span> === |
== <b><span style="color:#931136">A = [[1.8_Trigonometriska_kurvor#Amplitud.2C_frekvens_och_period|<span style="color:blue">Amplitud</span>]]</span></b> == | == <b><span style="color:#931136">A = [[1.8_Trigonometriska_kurvor#Amplitud.2C_frekvens_och_period|<span style="color:blue">Amplitud</span>]]</span></b> == | ||
== <b><span style="color:#931136">k = [[1.8_Trigonometriska_kurvor#Amplitud.2C_frekvens_och_period|<span style="color:blue">frekvens</span>]]</span></b> == | == <b><span style="color:#931136">k = [[1.8_Trigonometriska_kurvor#Amplitud.2C_frekvens_och_period|<span style="color:blue">frekvens</span>]]</span></b> == | ||
== <b><span style="color:#931136">b = [[1.9 Förskjutade trigonometriska kurvor|<span style="color:blue">förskjutning i x-led</span>]]</span></b> == | == <b><span style="color:#931136">b = [[1.9 Förskjutade trigonometriska kurvor|<span style="color:blue">förskjutning i x-led</span>]]</span></b> == | ||
== <b><span style="color:#931136">d = [[1.9 Förskjutade trigonometriska kurvor|<span style="color:blue">förskjutning i y-led</span>]]</span></b> == | == <b><span style="color:#931136">d = [[1.9 Förskjutade trigonometriska kurvor|<span style="color:blue">förskjutning i y-led</span>]]</span></b> == | ||
| − | === | + | === <span style="color:#931136">Exempel: Från grafen till ekvationen</span> === |
<div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 2_3_Ekv_sinusformad_kurvaNy_1a.jpg]] </div> | <div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 2_3_Ekv_sinusformad_kurvaNy_1a.jpg]] </div> | ||
</div> | </div> | ||
| Rad 31: | Rad 31: | ||
<div class="ovnC"> | <div class="ovnC"> | ||
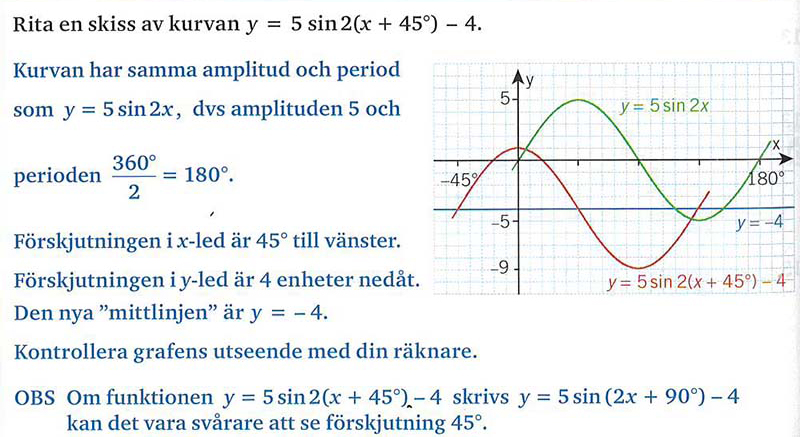
| − | === | + | === <span style="color:#931136">Omvänt problem: Från ekvationen till grafen</span> === |
<div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 2_3_Ekv_sinusformad_kurvaNy_2.jpg]] </div> | <div style="border:1px solid black;display:inline-table;margin-left: 10px;"> [[Image: 2_3_Ekv_sinusformad_kurvaNy_2.jpg]] </div> | ||
</div> | </div> | ||
Nuvarande version från 3 augusti 2025 kl. 16.07
Repetera Amplitud, frekvens och period
och Förskjutade trigonometriska kurvor.
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
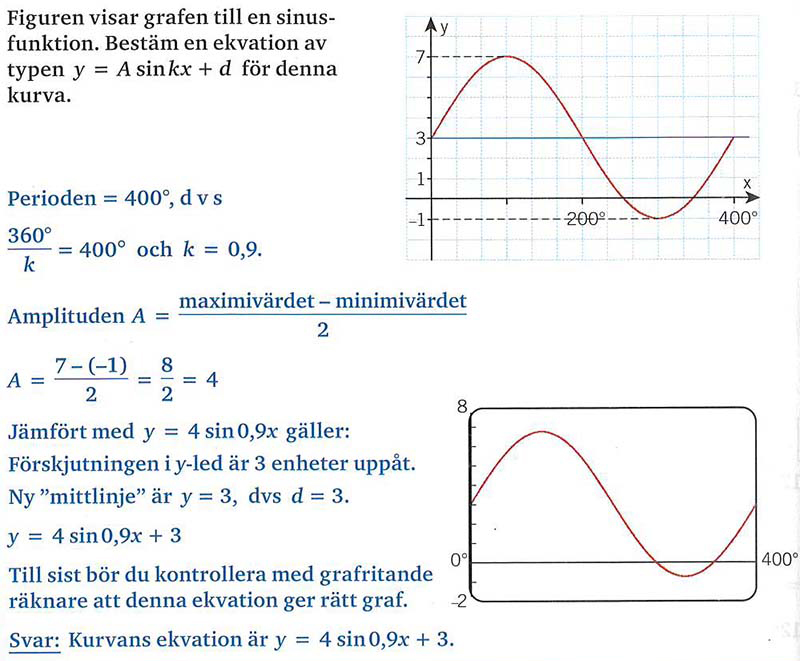
Kombinera amplitud, frekvens och förskjutning
Generellt: y = A sin k(x-b) + d
A = Amplitud
k = frekvens
b = förskjutning i x-led
d = förskjutning i y-led
Exempel: Från grafen till ekvationen
Omvänt problem: Från ekvationen till grafen
Copyright © 2024 Lieta AB. All Rights Reserved.
