Skillnad mellan versioner av "1.10 Rekursion"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 40: | Rad 40: | ||
<big>Rekursion används här som ett koncept för prblemlösnig: Hur gör jag för att med så få försök som möjligt gissa rätt i Gissa tal-spelet? Jag upprepar intervallhalvering. | <big>Rekursion används här som ett koncept för prblemlösnig: Hur gör jag för att med så få försök som möjligt gissa rätt i Gissa tal-spelet? Jag upprepar intervallhalvering. | ||
| − | Nu ska vi använda rekursion som ett koncept inom programmering. | + | Nu ska vi använda rekursion som ett koncept inom programmering, se [[1.10_Rekursion#Programmet_Fibonacci|<b><span style="color:blue">Programmet Fibonacci</span></b>]]. |
| − | I matematiken realiseras konceptet med s.k. <i>rekursionsformler</i>, se [[1.10_Rekursion#Fibonaccis_rekursionsformel|<b><span style="color:blue"> | + | I matematiken realiseras konceptet med s.k. <i>rekursionsformler</i>, se [[1.10_Rekursion#Fibonaccis_rekursionsformel|<b><span style="color:blue">Fibonaccis rekursionsformel</span></b>]]. |
</big> | </big> | ||
</div> | </div> | ||
Versionen från 17 december 2020 kl. 16.47
| << Lektion 16 | Genomgång | Övningar |
Vad är rekursion?
Ordet rekursion kommer från det latinska recurrere som betyder att köra igen. Dvs:
Man återvänder till något som man redan gjort en gång och upprepar ett känt förlopp,
kanske under andra förutsättningar.
Rekursion är ett koncept som används i problemlösning genom successiv upprepning.
Hittills har vi realiserat upprepning i programmering med loopar. Rekursion är ett alternativ till loopar.
Exempel på en rekursiv algoritm
Algoritmen Intervallhalvering
Optimal strategi för att med så få försök som möjligt gissa rätt i Gissa tal-spelet.
Körexempel på Gissa tal-spelet där algoritmen Intervallhalvering använts:
Rekursion används här som ett koncept för prblemlösnig: Hur gör jag för att med så få försök som möjligt gissa rätt i Gissa tal-spelet? Jag upprepar intervallhalvering.
Nu ska vi använda rekursion som ett koncept inom programmering, se Programmet Fibonacci.
I matematiken realiseras konceptet med s.k. rekursionsformler, se Fibonaccis rekursionsformel.
Annat exempel: Fibonacci
Kaniners fortplantning
Följer man Fibonaccis instruktioner för kaniners fortplantning får man följande siffror:
Fibonaccitalen
| Mönster för bildningen av Fibonaccis talföljd, även kallad Fibonaccitalen: Summan av två på varandra följande |
\( \qquad\qquad\qquad \) |
Fibonaccis rekursionsformel
Mer utförligt om om Fibonacciproblemet kan du läsa här.
Fibonaccis rekursionsformel kan direkt tas över till följande pythonprogram:
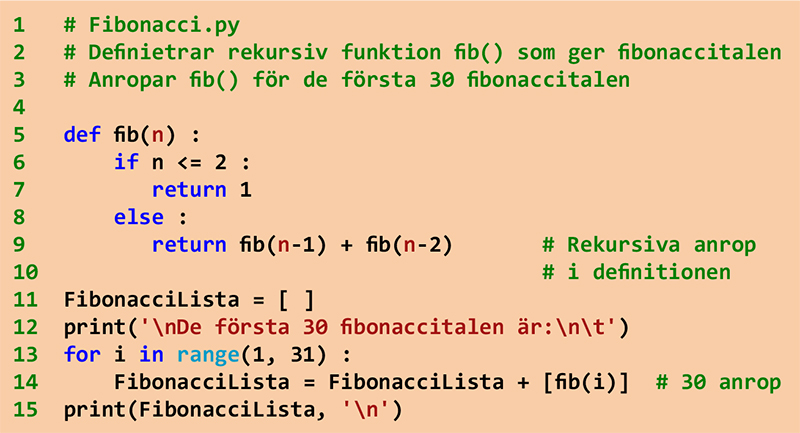
Programmet Fibonacci
I Python kan Fibonaccis rekursionsformel kodas som en rekursiv funktion fib().
En funktion kallas för rekursiv om den anropar sig själv i sin egen definition.
Funktionen fib() anropar sig själv två gånger i sin definition på rad 9: rekursiva anrop!
Anropet på rad 14 är ett vanligt (inte rekursivt) funktionsanrop i huvudprogrammet.
Körresultat
Läs om rekursion i kursboken på sid 98-100.