Skillnad mellan versioner av "1.10 Ekvationen för en sinusformad kurva"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 1: | Rad 1: | ||
__NOTOC__ | __NOTOC__ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
| Rad 16: | Rad 9: | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| + | |||
| + | |||
| + | <big><big><b> | ||
| + | Repetera [[1.8_Trigonometriska_kurvor#Amplitud.2C_frekvens_och_period|<span style="color:blue">Amplitud, frekvens och period</span>]] | ||
| + | |||
| + | och [[1.9 Förskjutade trigonometriska kurvor|<span style="color:blue">Förskjutade trigonometriska kurvor</span>]]. | ||
| + | </b></big></big> | ||
Nuvarande version från 9 september 2025 kl. 06.55
| << Förra avsnitt | Genomgång | Övningar | Facit | Nästa avsnitt >> |
Repetera Amplitud, frekvens och period
och Förskjutade trigonometriska kurvor.
Kombinera amplitud, frekvens och förskjutning
Generellt: y = A sin k(x-b) + d
A = Amplitud
k = frekvens
b = förskjutning i x-led
d = förskjutning i y-led
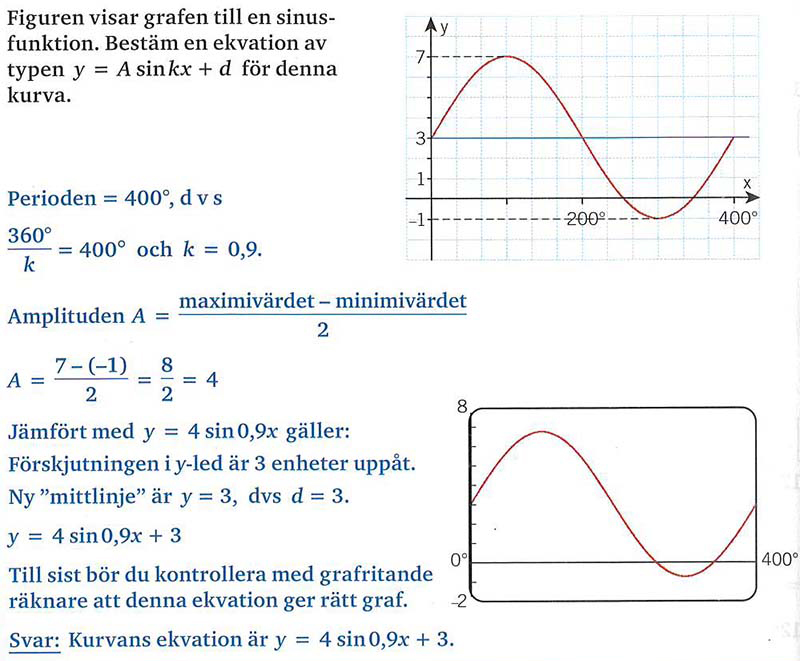
Exempel: Från grafen till ekvationen
Omvänt problem: Från ekvationen till grafen
Copyright © 2024 Lieta AB. All Rights Reserved.
